2. Моделирование внутривидовой и межвидовой конкуренции.

Реальные популяции в природе всегда существуют во взаимоотношениях (с другими популяциями). Эти взаимоотношения могут быть конкурентные или трофические (например, системы "хищник- жертва"). В случае конкуренции близко родственных видов коэффициенты скорости роста численности каждой i- ой популяции должны зависеть от численности X=X(T) другого вида, т.е.

(6)

Например, для двух видов будем иметь следующую систему уравнений:

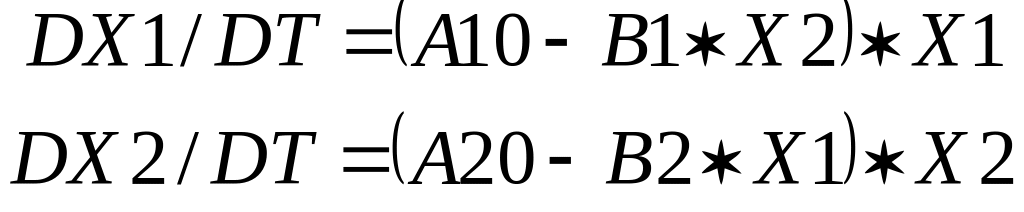_{, (7)}

т.е. здесь на численность 1-ой популяции влияет численность 2-й (-B1X2), а на 2-ю - численность-1-й (-B2X1 ). Такие системы уравнений будут представлять конкуренцию близко родственных видов, которые (как показывает исследование системы (7)) не могут устойчиво существовать в одной экологической нише. На это указывал еще Дарвин, который доказал, что конкуренция близко родственных видов- самая жестокая. Другое дело трофические взаимоотношения в системах "хищник-жертва" (или "паразит-хозяин"). Такие системы в природе довольно устойчивы, а их динамика в большинстве случаев должна иметь колебательный характер. Например, если численность жертвы X, а численность хищника Y=Y(T), то их динамика будет описываться следующей системой уравнений:

(8)

Здесь положительное A1 показывает свободное размножение жертвы, а "-B1*Y"- ее поедание хищником. Соответственно, хищник сам по себе вымирает (-A2),но за счет численности жертвы (+B2X) может поддерживать свою численность. Уравнения (8) могут быть приведены к следующему рекуррентному вида:

(9)

которые можно решить с помощью ЭВМ (см. приложение 2). Здесь символ  , означает умножение сомножителей. Динамика поведения Х и  показана на рис. 3. Легко видеть, что существует сдвиг по фазе между кривыми.

Рис. 2. Динамика поведения системы хищник- жертва

(паразит- хозяин).

Приложение 2.

Динамика поведение 2-х взаимодействующих видов типа “хищник- жертва” (или “паразит- хозяин”) описывается уравнениями (8) и (9), т.е.

(10)

Здесь жертва (XN) размножается со скоростью А1, но поедается со скоростью (–B1YS) и наоборот, хищник (YN) сам вымирает (A2) и стимулируется пищей (В2XS). Программа, реализующая систему (10) на экране монитора имеет вид (с учетом замечаний в Приложении 1):

10 CLS: SCREEN 9, 1, 0

20 INPUT “A1=”, A1: INPUT “A2=”, A2; INPUT “B1=”, B1:

INPUT B2=,B2

21 INPUT “X0=”, X0: INPUT “Y0=”, Y0: INPUT “DT=”, DT:

INPUT K=,K

30 XS = X0+ (A1- B1  Y0) X0  DT:

YS = Y0 + (-A2+B2  Х0)  Y0  DT

40 FOR I=2 TO K

50 XN=XS+(A1-B1YS)XSDT: YN=YS+(-A2+B2ХS)YSDT:

Т=DTI+50

60 X =200 - XN: PSET (T, X), 14: Y=200 -YN: PSET(T,Y), 12

70 XS=XN: YS=YN: NEXT I

80 LINE (50, 200) - (50, 20),12:LINE (50, 200) - (600, 200), 12

90 LOCATE 3,4: PRINT “численность X и Y”:

LOCATE 23,62: PRINT “реальное время T”

100 LOCATE 24,4 : PRINT “ Динамика численности хищника и жертвы (X)”

Задание 2.

Наберите эту программу на ЭВМ. Задайте приблизительно (гипотетически) начальные условия модели (10): A1=0.3, B1=0.006, X0=50, Y0=20, K=60000, DT=0.01. Зарисуйте график с экрана монитора. Охарактеризуйте динамику жертвы (желтая линия) и хищника (красная). Измените несколько раз В2 и охарактеризуйте процесс после изменений. Приведите примеры реальных двухвидовых экосистем.