Блок информации

Стационарные режимы функциональных систем организма.

Организм человека – это совокупность многих функциональных систем. Эти системы испытывают постоянные возмущения со стороны внешней и внутренней среды. Центральная нервная система (ЦНС) обеспечивает некоторую стабильность работы всех этих функциональных систем. Например, работа сердца, частота дыхания в норме приблизительно находятся около некоторого стационарного состояния. Математически это выглядит так, что скорости изменения параметров x этих систем (dx/dt) приблизительно равны нулю (т. е. dx/dt=0 или x=const).

Однако внешние возмущения приводят к dx/dt0. Возникает вопрос: как оценить момент, когда мы переходим от x=const к x=x(t), т.е. xconst? Ответ на этот вопрос представлен в данной работе.

1. Понятие динамических систем в живой и неживой природе.

Любая техническая или биологическая система может быть описана некоторыми переменными величинами, которые можно трактовать как координаты некоторого вектора состояния х данной БДС, т.е.

,

где х – вектор-столбец, х^т – вектор-строка, x_i = x_i(t).

Координаты x_i(i=1,2, ... ,n) такого вектора могут иметь различный смысл. Например, для движущегося механизма x_i- это его координаты в пространстве (X,Y,Z) и во времени t, а так же величины изменения переменных (x,y,z) во времени, т.е. скорости dx/dt = V_x, dy/dt= V_y, dz/dt= V_z. Зная эти семь переменных мы можем характеризовать полностью движение любого тела в пространстве.

Отметим, что в этом примере x₁=x, x₂=y, x₃=z, x₄=V_x, x₅=V_y, x₆=V_z являются функциями (переменными) от аргумента t, т.е. вектор x=(x₁,x₂,...,x₆) состоит из 6-ти компонент. Его можно представить в виде вектора в 6-ти мерном пространстве, но графически это сделать трудно. Тем не менее мы будем говорить в дальнейшем о задании любого вектора x состояния БДС в n-мерном пространстве, которое будем называть фазовым пространством. Например, если мы имеем дело с функциональной системой (ФС) организма (по П. К. Анохину ФС – это комплекс взаимодействующих компонентов для получения полезного для организма результата), то она описывается своими переменными величинами. Одной из основных ФС человека является кардио-респираторная система (КРС), которая обеспечивает адаптивную реакцию организма на увеличение физической нагрузки или при эмоциональных стрессах. В этих случаях компонентами вектора состояния x ФС будут величины частоты сердечных сокращений (ЧСС), систолическое (САД) и диастолическое (ДАД) артериальное давление (АД), показатели электрокардиографии (ЭКГ), частоты и глубины дыхания и т.д. Все эти компоненты x_i характеризуют КРС как в покое, так и при нагрузках. Понятно, что в покое x_iconst, т.е. dx/dt0 [3].

2. Стационарные режимы биологических динамических систем (бдс).

Их классификация.

Описание динамики поведения ФС может быть представлено в виде системы дифференциальных или разностных уравнений (ДУ и РУ), например, в виде

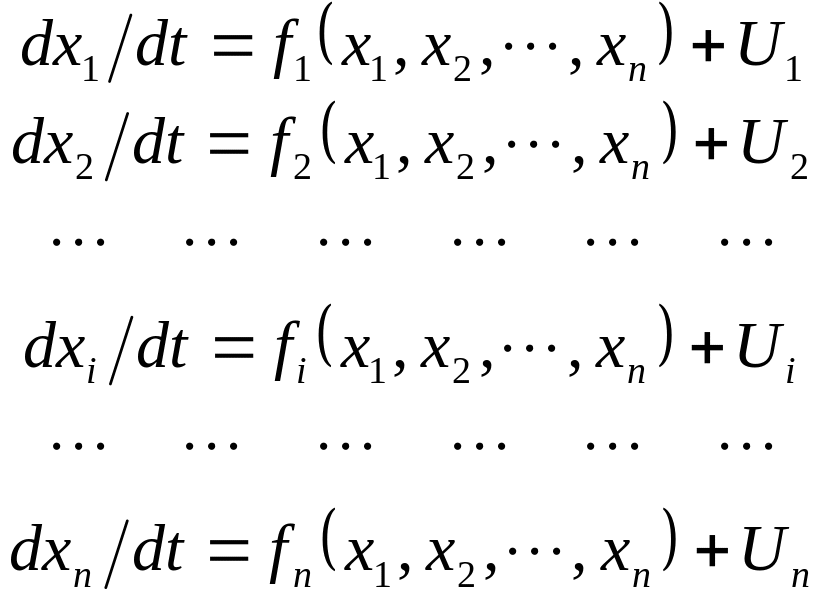, (1)

где f_i(x₁, x₂, ..., x_n)- некоторые функции, а U_i– учитывает внешние воздействия на ФС.

Отметим, что (1) можно записать в векторной форме dx/dt=Ax+U, где A является некоторой матрицей, элементы a_ij, которой представляют величины воздействия j-й компоненты вектора x на i-й компоненту. Например, модель вида

(2)

имеет матрицу , вектор x^Т=(x₁,x₂), вектор U^Т=(U₁, U₂). Она может описывать реципрокные взаимодействия в ЦНС или мышечной системе (между мышцами- агонистами, т.е. флексорами-экстензорами). Модель (2) использовалась Н.Рашевским для моделирования поведения водителя за рулем автомобиля. Важно отметить, что в стационарном состоянии (dx/dt=0) система (1) переходит в систему обыкновенных (алгебраических) уравнений, из которой можно определить координаты (x_0i) точки покоя (ТП) x₀.

Очевидно, что в биологии может быть x₀=0 (полный покой, если внешние возмущения U_i=0) или x₀>0. Например, если человек не испытывает нагрузки, то ЧСС (n) и АД (P) могут быть (x₁=n, x₂=P) постоянными, т.е. x₀₁=C₁, x₀₂=C₂.

Итак, возможны нулевые и ненулевые значения x₀. Для модели (2) x₀>0 всегда, если U>0 (докажите!). Это значит, что для открытых (с внешним драйвом) систем их стационарные состояния ненулевые. Полное описание точек покоя модели (2) и их представление на фазовой плоскости (возможны ТП типа узла, фокуса, седла и др.) представлено в приложении 1 и демонстрируется в специальном файле TPF.exe. Важно отметить, что эти ТП могут быть устойчивыми и неустойчивыми. В первом случае внешние возмущения в БДС выводят её из состояния равновесия, в которое БДС возвращается спустя некоторое время (например, устойчивый фокус). Во втором случае траектория на фазовой плоскости с течением времени уходит в бесконечность- система неустойчива.