1.30. Применение метода анализа размерностей
Формулы Вейсбаха — Дарси и Вейсбаха и некоторые другие соотношения гидравлики могут быть получены из апалпза размерностей. В основе ;>того метода лежит так называемая Пн-теорема, пли теорема Бакингема, которая заключается в следующем: функциональная зависимость между п физическими размерными величинами всегда может быть преобразована в уравнение, содержа-
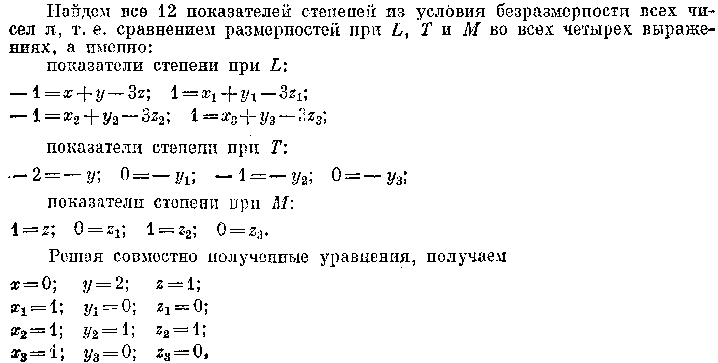
м-
А\
Ртр
р^ "=ЧЧ
d
;
rfyp
:
d/*
или, учитывая
пропорциональность между Pрт
и l/d
и выражение числа Рейнольдса, находим
V
/ Д Ф, 1 Re,
-^
, Глава 7. МЕСТНЫЕ
ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ
1.31
Общие сведения о местных сопротивлениях
Выше указывалось
(см. п. 1,17), что гидравлические потери
энергии делятся па местные потери
и потери па трение по длине. Потеря на
трение в прямых трубах постоянного
сечения рассмотрены при ламинарном
(см. гл. 5) и турбулентном (см- гл. б)
течениях. Рассмотрим потери, обусловленные
местными гидравлическими сопротивлениями,
т. е. такими элементами трубопроводов,
в которых вследствие изменения размеров
пли конфигурации русла происходит
изменение скорости потока, отрыв
транзитного потока от стенок русла и
возникают вихреобразования.
В п. 1.17 были
приведены примеры некоторых местных
сопротивлений и дана как эмпирическая
общая формула связи местной потери
напора и скорости потока, т. е. формула
(1.57) Вейсбаха;
аким
образом» теперь вместо выражении (1.105)
мы можем записать
Обозначив функцию ^L через Хт, окончательно получим
h -I l v"
Таким образом, получили формулу Венсбаха — Дарси, а также информацию о том, какими факторами определяется коэффициент Дарси λт.
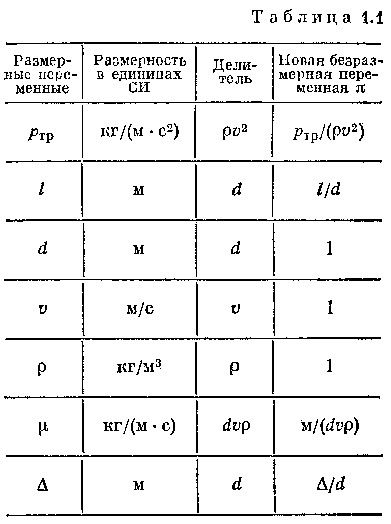
К тому же результату можно прийти, если вместо решения системы из 12 уравнений составить таблицу, содержащую первоначальные размерные переменные, их размерности, затем делители, подобранные из условия получении безразмерных переменных, и, на-конец, новые безразмерные переменные (табл. 1.1).
Обращение в единицу трех новых переменных я и влечет за собой уменьшение числа переменных на три.