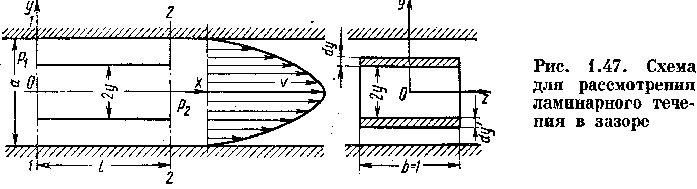
1.26. Ламинарное течение в зазоре между двумя стенками и в прямоугольных трубах

Рассмотрим ламинарное течение в зазоре, образованном двумя параллельными плоскими стенками, расстояние между которыми равно а (рис. 1.47). Начало координат поместим в середине зазора, направив ось Ох вдоль течения, а ось Oy — по нормали к стенкам.

Возьмем два нормальных поперечных сечения потока на расстоя­нии I одно от другого и рассмотрим поток шириной, равной еди­нице. Выделим объем жидкости в форме прямоугольного паралле­лепипеда, расположенного симметрично относительно оси Ох между выбранными поперечными сечениями потока и имеющего размеры сторон I X 2у X 1.

Запишем условие равномерного движения выделенного объема вдоль оси Ох:

где р_тр = р1_г — р2 - разность давлений (перепад) в рассматривае­мых сечений.

Знак минус обусловлен тем, что производная dv/dy отрица­тельна .

Из предыдущего найдем приращение скорости dv_, соответствую­щее приращению координаты dy:

После интегрирования получим

Так как при у — а/2 v =0, находим откуда

Далее подсчитаем расход q, приходящийся па единицу ширины потока, для чего возьмем симметрично относительно оси Oz две элементарные площадки размером 1 X dy и выразим элементарный расход

стоянно вдоль длины, подвижная стенка увлекает за собой жидкость, и возникает так называемое фрикционное безнапорное дви­жение. Выделим в таком потоке элемент, как показано на рис. 1.48, и рассмотрим действующие на него силы. Так как давления р, при­ложенные к левой и правой граням элемента, одинаковы, то для рав­новесия сил необходимо, чтобы касательные напряжения на нижней и верхней гранях были бы также одинаковы, т. е. т — const.

После подстановки С и С₁ в последнее уравнение получим за­кон распределения скоростей

(1.90)

Расход q жидкости, приходящийся на единицу ширины зазора, определится по средней скорости

(1.91)

Если же указанное перемещение стенки происходит при пере­паде давления в жидкости, заполняющей зазор, то закон распре­деления скоростей в нем найдем как сумму (или разность в зависи­мости от направлении движения стенки) выражений (1.87) и (1.90):

Выразим потерю давления на трение через полный расход Q = qb в зазоре шириной b не равно1 ; получим

(1,89)

Когда одна из стенок образующих зазор, перемещается в на­правлении, параллельном другой стойко, а давление в зазоре по-

Распределение скоростей в зазоре показано на рис. 1.49 в двух вариантах: а) направление движения стенки совпадает с направ­лением течения жидкости под действием перепада давлений; б) на­правление движения стенки противоположно течению жидкости.

Расход жидкости через зазор единичной ширины в этих случаях определится как сумма расходов, выражаемых формулами (1.88) и (1.91), т. о.

Первое слагаемое формулы называется расходом напорного тече­ния, а второе — фрикционным расходом.

Приведенным выражением можно также пользоваться в том слу­чае, когда зазор образован двумя цилиндрическими поверхностями» например поршнем и цилиндром, при условии, что зазор между

Рис. 1.50. Схемы концентричного и экс­центричного зазоров

ними мал по сравнению с диа­метрами поверхностей, и по­верхности расположены соосно (рис. 1.50, а).

Если поршень расположен: в цилиндре с некоторым экс­центриситетом (рис. 1.50, б), то зазор а между ними будет пере­менной величиной:

Рассматривал элемент зазора шириной rdφ как плоскую щель, получим следующее выражение для элементарного расхода:

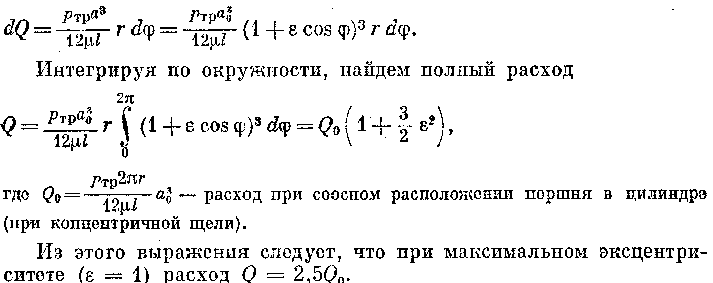
При расчетах течений жидкости в трубах с некруглым попереч­ным сечением используют так называемый гидравлический. радиус, равный отношению площади сечения к его смоченному периметру П; Rг = S/II, или гидравлическим диаметром D_r = 4R_r (для круглого сечения гидравлический диаметр равен геометрическому: D_r = d).