13) Волны де Бройля. Статистический смысл волн де Бройля, свойства волн

Волны де Бройля — волны, связанные с любой микрочастицей и отражающие их квантовую природу. Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект - корпускула, но и как волна, причём длина этой волны даётся формулой = h/р, где h = 6.6^.10^-34 Дж^.сек – постоянная Планка, а р – импульс частицы. Эта волна и получила название волны де Бройля.

Согласно статистической интерпретации волны де Бройля следует рассматривать как волны вероятности. Более определенно: интенсивность волны де Бройля в каком-либо месте пространства пропорциональна вероятности обнаружить частицу в этом месте.

Свойства волн де Бройля:

1) Фазовая скорость волны де Бройля вычисляется в результате дифференцирования этого уравнения по времени: E – p dx/dt = 0,. υ_ф = dx/dt = E/p = mc²/mυ = c c/υ, где υ-скорость частицы. Т.к. υ<c, то фазовая скорость волн де Бройля всегда больше скорости света в вакууме, т.е. υ_ф > c.

Это соотношение отражает особое специфическое свойство волн де Бройля.

2) Групповая скорость волн де Бройля равна скорости движения частиц: υ_r = ds/dt = υ.

3) Длинам боровских орбит соответствуют стоячие волны де Бройля, т.е. в длину боровской орбиты укладывается целое число стоячих волн де Бройля: 2πr_n = nλ.

14) Соотношение неопределенностей.

Принцип неопределённости Гейзенберга - в квантовой механике так называют принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы.

Соотношения неопределённости Гейзенберга — это теоретический предел точности любых измерений. Они справедливы для так называемых идеальных измерений, иногда называемых измерениями фон Неймана. Они тем более справедливы для неидеальных измерений или измерений Ландау.

Соответственно, любая частица (в общем смысле, например несущая дискретный электрический заряд) не может быть описана одновременно как «классическая точечная частица» и как волна. (Сам факт того, что какое-либо из этих описаний может быть справедливо, по крайней мере в отдельных случаях, называют корпускулярно-волновым дуализмом). Принцип неопределённости, в виде, первоначально предложенном Гейзенбергом, верен в случае, когда ни одно из этих двух описаний не является полностью и исключительно подходящим, например частица в коробке с определённым значением энергии; то есть для систем, которые не характеризуются ни каким-либо определённым «положением» (какое-либо определённое значение расстояния от потенциальной стенки), ни каким-либо определённым значением импульса (включая его направление).

Соотношение неопределенности Гейзенберга показывает, что “между точностью, с которой одновременно может быть установлено положение частицы, и точностью ее импульса существует определенное соотношение”: q p ≥ h ,

где - среднеквадратичное отклонение.

15. Волновая функция: её свойства и смысл

16.Уравнение Шредингера общее и стационарное.

Стационарное уравнение Шредингера для движения электрона в кулоновском поле ядра атома водорода и водородоподобных атомов имеет вид: ∆ψ + (8π²m/h²)(E-U)Ψ = 0,

где Ψ – волновая функция, ∆ - оператор Лапласа, Е – полная энергия электрона в атоме, U = -(Ze²/4πε₀r) – потенциальная энергия.

потенциалом V(r,t)

17) Частица в потенциальной яме.

Потенциальная яма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.

Используя граничные условия, имеем:

Ψ_{(x = 0)} = a sin α = 0 Отсюда, α = 0

Ψ_{(x = 1)} = a sin ωl = 0 Отсюда, ωl = ± nπ (n = 1,2, …)

Учитывая значения ω, получим:

E_n = ħ²π²/2ml n² (n = 1, 2, …)

E_n – собственны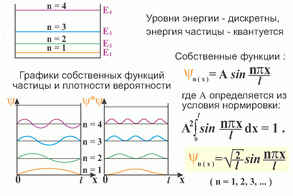 е значения энергии.