Задача № 28

Груз, лежащий на середине упругой балки, прогибает ее на величину δ_СТ (статический прогиб балки). Пренебрегая весом балки, определить, чему будет равен ее максимальный прогиб δ_m, если груз упадет на балку с высоты Н.

Д ля решения задачи используем дважды теорему об изменении кинетической энергии.

Участок М₀М': определяем скорость в точке М'

V₀ =0

Участок М'M₀:

V₁ = 0

Вычисляем работу сил: сила тяжести

сила упругости ,

где

с – коэффициент упругости, который определяем из условия

Таким образом

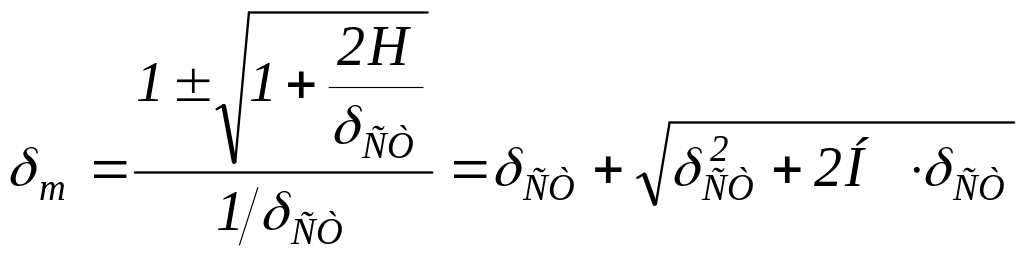
Задача № 29

Колесо массы М вращается вокруг оси О с угловой скоростью ω₀. В некоторый момент колесу прижимается тормозная колодка с силой Q. Коэффициент трения колодки о колесо равен f, радиус колеса равен r. Пренебрегая трением в оси и массой спиц, определить через сколько секунд колесо остановится.

Используем дифференциальное уравнение вращательного движения

где момент инерции колеса

сила трения

Таким образом

Для определения времени до остановки разделяем переменные и интегрируем дифференциальное уравнение в пределах при

в конце движения

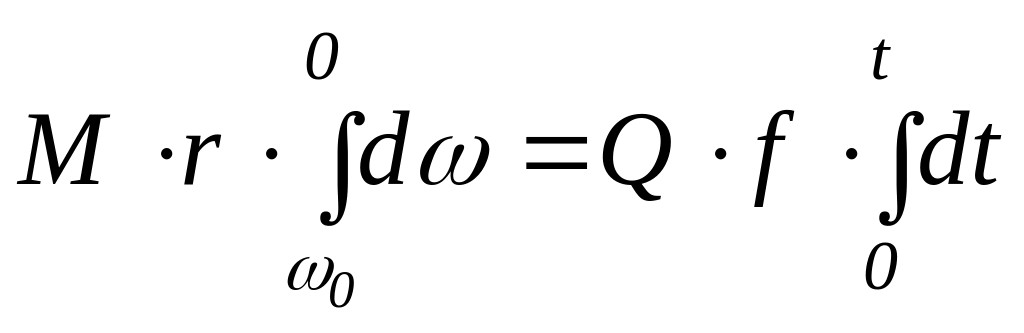
Задача № 30

Определить силу, стремящуюся разорвать равномерно вращающийся маховик массы М, считая его массу распределенной по ободу. Радиус маховика равен r, а угловая скорость ω.

Д ля решения задачи используем принцип Даламбера. К действующим активным силам добавляем силы инерции и теперь система находится в равновесии.

Силы инерции элементарных частиц заменяем равнодействующей

где

Уравнение равновесия