Задача № 15
На барабан весом Р и радиусом r намотана нить с грузом А весом Q на конце. Пренебрегая массой нити и трением в оси, определить угловое ускорение барабана при вертикальном движении груза, если радиус инерции барабана относительно его оси ρи.
Используем теорему об изменении
кинетической энергии в дифференциальной
форме
Изображаем систему вместе с действующими на нее внешними силами:
активными – силы тяжести
реакциями связей –
Определяем кинетическую энергию системы
Груз А
поступательное движение
Барабан В
вращательное движение
Момент инерции:
Скорость груза А
V выражаем через
угловую скорость барабана
Таким образом кинетическая энергия системы
Откуда
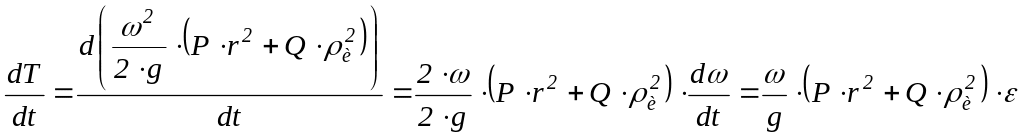
Определяем мощность внешних сил, приложенных к системе:
работу производит только сила тяжести Q
Таким образом получаем
Задача № 16
Вычислить кинетическую энергию кулисного механизма, если момент инерции кривошипа ОА относительно оси вращения, перпендикулярной плоскости рисунка, равен J0; длина кривошипа равна а, масса кулисы равна m, массой камня А пренебречь. Кривошип ОА вращается с угловой скоростью ω. При каких положениях механизма кинетическая энергия достигнет наибольшего и наименьшего значения.
Определяем кинетическую энергию
кулисного механизма
Кривошип ОА
вращательное движение
Кулисный камень А – массой камня пренебрегаем Т2 = 0
Кулиса
поступательное движение
Скорость кулисы определяем по векторному уравнению:
,
где
горизонтальный
вектор;
вектор перпендикулярный ОА;
вектор относительной скорости вертикальный
вектор.
С плана скоростей
Получаем
Кинетическая энергия достигнет
наибольшего значения при
равном 90 или 270 град.
Кинетическая энергия достигнет наименьшего значения при равном 0 или 180 град.
Задача № 17
Вычислить кинетическую энергию гусеницы трактора, движущегося со скоростью V0. Расстояние между осями колес равно L, радиусы колес равны r, масса одного погонного метра гусеничной цепи равна γ.
Определяем кинетическую энергию
кулисного механизма
Участок АВ
длина
;
масса
;
кинетическая энергия
,
где
Участок CD
кинетическая энергия
,
Участок ВC
длина
;
масса
;
кинетическая энергия
,
где
Получаем
Задача № 18
На вал диаметра 60 мм. насажен маховик диаметра 50 см., делающий 180 об/мин. Определить коэффициент трения скольжения f между валом и подшипником, если после выключения привода маховик сделал 90 оборотов до остановки. Массу маховика считать равномерно распределенной по его ободу. Массой вала пренебречь.
Используем
теорему об изменении кинетической
энергии в конечной форме
,
где Т = 0 – кинетическая энергия маховика в конце движения;
Т0 – кинетическая энергия маховика в начале движения;
сумма работ действующих сил
Кинетическая энергия маховика
,
где момент инерции маховика
масс маховика равномерно
распределена по его ободу;
угловая скорость маховика
работа сил трения между валом и
подшипником
,
где момент сил трения
угол поворота маховика за время
движения
Таким образом получаем
Окончательно
