Задача № 1
Автомобиль массы 1000 кг. движется по
выпуклому мосту со скоростью V
= 10 м/с. Радиус кривизны в середине
моста
м. Определить силу давления автомобиля
на мост в момент прохождения его через
середину моста.
Считая автомобиль материальной точкой, составляем дифференциальные уравнения движения в проекциях на оси естественной системы координат
,
где
Таким образом:
и
Задача № 2
Грузовой автомобиль массы 6000 кг. въезжает на паром со скоростью 6 м/с. Заторможенный с момента въезда на паром автомобиль остановился, пройдя 10 м. Считая движение автомобиля равнозамедленным, найти натяжение каждого из двух канатов, которыми паром привязан к берегу. При решении задачи пренебречь массой и ускорением парома.
Считая автомобиль материальной точкой, составляем дифференциальное уравнение движения в проекциях на ось Х, совпадающую с направлением движения автомобиля с паромом
,
где
Таким образом:
и преобразуем
Интегрируем
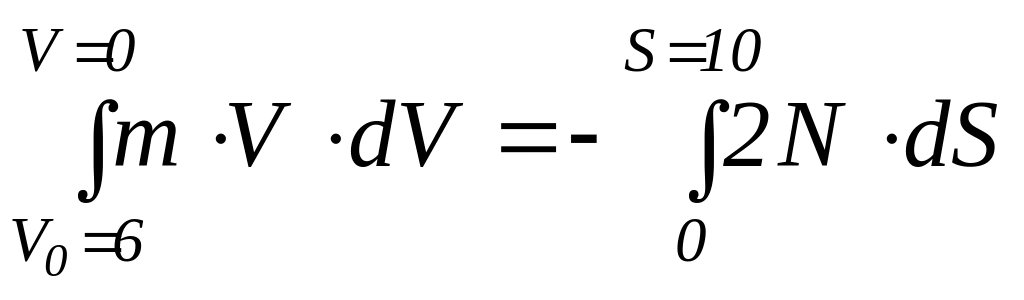
Задача № 3
Камень падает в шахту без начальной скорости. Звук от удара камня о дно шахты услышан через 6,5 с. от момента начала его падения. Скорость звука равна 330 м/с. Найти глубину шахты.
С
оставляем
дифференциальное уравнение движения
в проекциях на вертикальную ось Y
,
где
Таким образом:
и
Интегрируем
Еще раз интегрируем
,
где h – глубина шахты
Время движения звука
Теперь время падения камня
Получаем
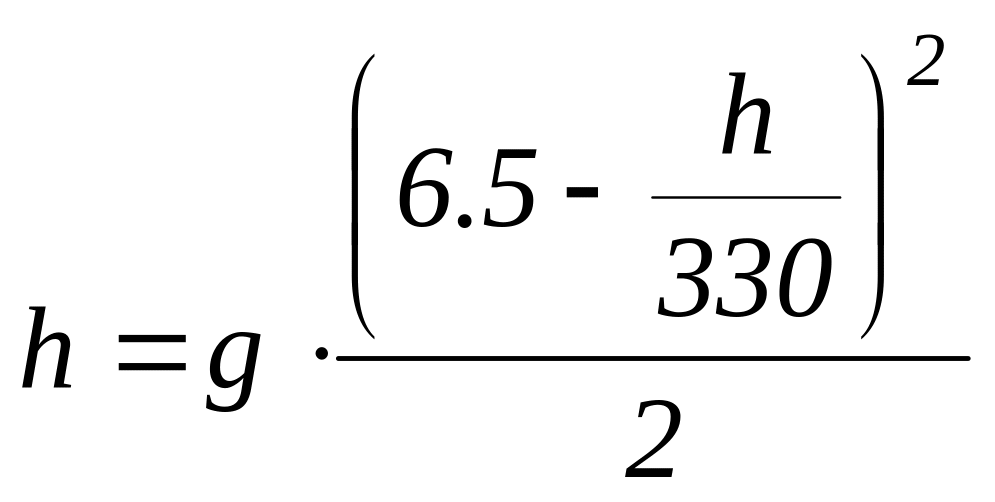
Задача № 4
Тело массы m вследствие полученного толчка прошло по негладкой горизонтальной плоскости за 5 с. расстояние S = 24.5 м. и остановилось. Определить коэффициент трения f.
Составляем дифференциальное уравнение движения в проекциях на горизонтальную ось Х
,
где
Таким образом:
и
Интегрируем
Еще раз интегрируем
Получаем
Задача № 5
Найти наибольшую скорость падения шара
массы 10 кг. и радиуса r
= 8 см, принимая, что сопротивление
воздуха равно
,
где V – скорость
движения,
площадь проекции тела на плоскость,
перпендикулярно направлению его
движения, и k –
численный коэффициент, зависящий от
формы тела и имеющие для шара значение
0,24 Н·с2/м4.
С
оставляем
дифференциальное уравнение движения
в проекциях на вертикальную ось Y
,
где
Таким образом:
и
Максимальная скорость будет при
Задача № 6
Гирька М привязана к концу нерастяжимой нити МОА, часть которой ОА пропущена через вертикальную трубку; гирька движется вокруг оси трубки по окружности радиуса МС = R, делая 120 об/мин. Медленно втягивая нить ОА в трубку укорачивают наружную часть нити до длины ОМ1, при которой гирька описывает окружность радиусом R/2. Сколько оборотов в минуту делает гирька по этой окружности?
Д
ля
решения задачи применяем закон сохранения
момента количества движения точки
относительно вертикальной оси, так как
действующие на гирьку силы не дают
момента относительно центральной
вертикальной оси, т.е.
.
Поэтому момент количества движения
гирьки относительно центральной оси
постоянный.
Получаем
Скорость точки М
Скорость точки М1
Получаем
Задача № 7
Каков должен быть коэффициент трения f колес заторможенного автомобиля о дорогу, если при скорости езды V = 20 м/с. он останавливается через 6 с. после начала торможения.
Для решения задачи применяем теорему об изменении количества движения точки в проекциях на ось, совпадающую с линией движения автомобиля.
,
где V = 0 – скорость автомобиля в конце торможения;
V0 = 20 м/с – скорость автомобиля в начале торможения;
Fтр = mg·f – сила трения
,
,
Задача № 8
Точка совершая равномерное движение по окружности со скоростью V=0,2 м/с., делая полный оборот за время Т=4 с. Найти импульс S сил, действующих на точку, за время одного полупериода, если масса точки m=5 кг. Определить среднее значение силы F.
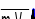
Для решения задачи применяем теорему об изменении количества движения точки в векторной форме
,
где V1 = V2 = V = 0.2 м/c – точка совершает равномерное движение;
S = F·t – импульс силы
По чертежу видно. что
,
Среднее значение силы F
Задача № 9
Определить мощность двигателя продольно-строгального станка, если длина рабочего хода 2 м., его продолжительность 10 с., сила резания 11,76 кН., коэффициент полезного действия станка 0,8. Движение считать равномерным.
Работа силы резания
Мощность, затрачиваемая для преодоления
силы резания
Мощность двигателя
Задача № 10
Гвоздь вбивается в стену, оказывающую сопротивление 700 Н. При каждом ударе молотка гвоздь углубляется в стену на длину l = 0.15 см. Определить массу молотка, если при ударе о шляпку гвоздя он имеет скорость V = 1,25 м/с.
Используем теорему об изменении кинетической энергии для материальной точки.
,
где
кинетическая энергия молотка в начале
движения гвоздя;
кинетическая энергия молотка в конце
движения гвоздя;
работа,
затрачиваемая на перемещение гвоздя
,
Задача № 11
Горизонтальная трубка CD равномерно вращается вокруг оси АВ с угловой скоростью ω. Внутри трубки находится тело М. Составить дифференциальное уравнение движения тела в трубке, если коэффициент трения скольжения между телом и трубкой равен f.
Д
ля
получения дифференциального уравнения
относительного движения точки М к
действующим силам надо добавить силы
инерции пререносного движения и
Кориолиса.
Сила инерции переносного движения при
равна
,
где
Сила инерции Кориолиса равна
,
где
Сила трения
Дифференциальное уравнение относительного движения точки М имеет следующий вид:
