4.3. Расчеты на прочность при изгибе. Проверка прочности балок, подбор сечений и определение допускаемой нагрузки.

Задача 12.

Балка двутаврового поперечного сечения (рис. 20а) шарнирно оперта по концам и нагружена сосредоточенной силой и сосредоточенным моментом. Проверить прочность балки, если F=20 кН, М=30 кНм, Ϭ_т=180 МПа.

Решение.

Изображаем расчетную схему рис. 19б, отбросив опоры и заменив их действие на балку опорными реакциями R_А и Rв, которые наносим на схему и определяем из уравнений равновесия статики.

1. ΣМ_А(Fi)=М-F3+Rв5=0

2. ΣMв(F_i)=М+F2-R_А 5=0

Определяем опорные реакции R_A и Rв

Из (1) уравнения Rв =

_{Из (2) уравнения RA=}

Проверим правильность найденных опорных реакций, так как ошибка на этой первоначальной стадии решения задачи, приводит к ошибочному решению всей задачи.

Для проверки спроектируем все силы на ось y:

ΣFiy=R_А-F+Rв=14-20+6=0

Реакции определены правильно.

Построение эпюры Q. Определяем расчетные участки. Границами участков являются точки приложения заданного сосредоточенного момента М (точка С), сосредоточенной силы F (точка D). Здесь три расчетных участка (АС, СD, DВ).

Участок АС. 0≤Z₁≤1. Начало отсчета координаты Z выбрано в точке А. слева от сечения расположены одна сила R_A, которая сдвигает левую часть балки вверх. Следовательно, поперечная сила в этом сечении Q=R_A=14 кн. Эпюра Q – прямая, параллельная оси Z.

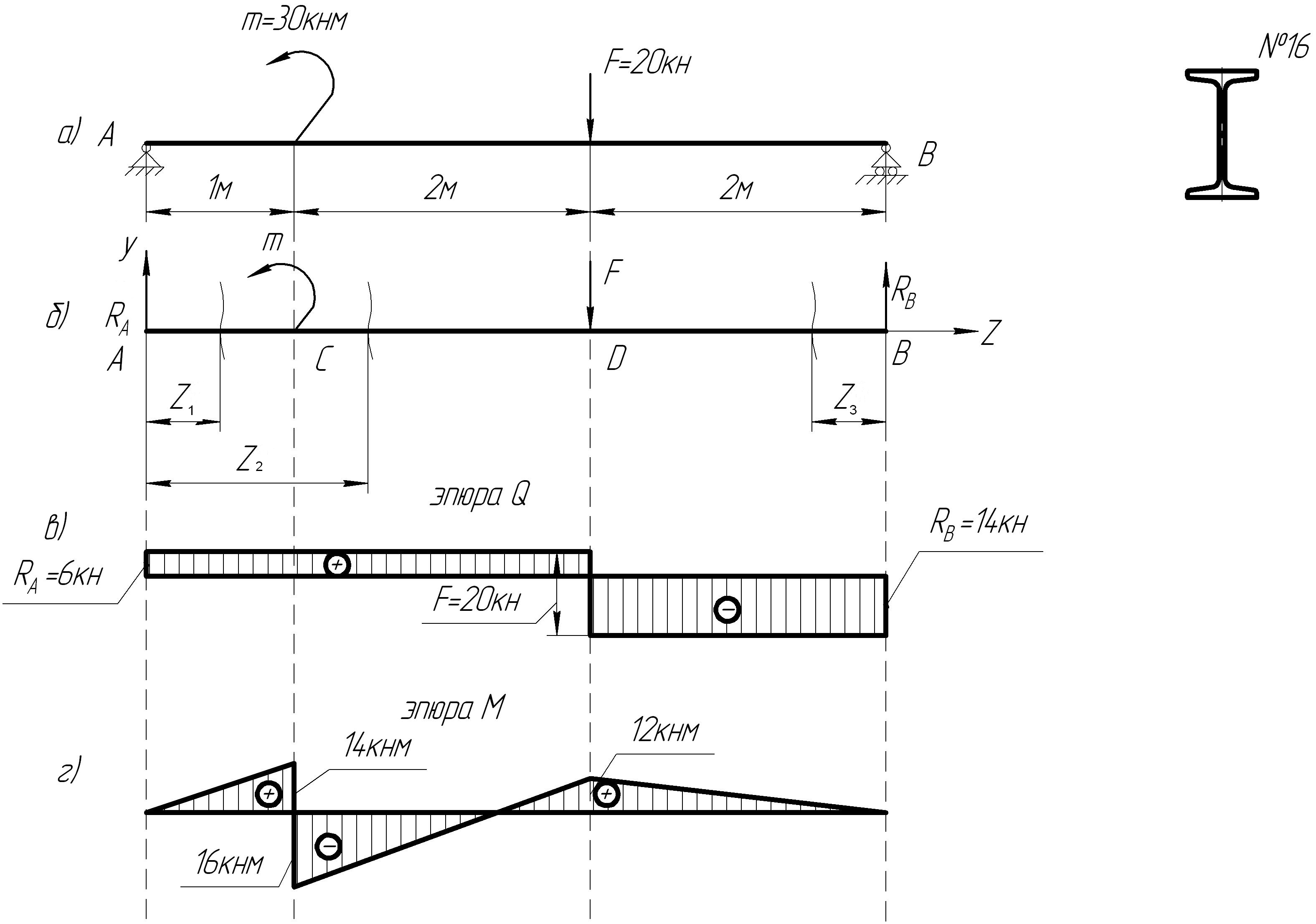
Рис. 20

Участок СD. 1≤Z₂≤3. Для этого участок начало координат остается по прежнему в сечении А. слева от сечения приложены R_A и М. Так как момент не сдвигает балку вверх или вниз, поперечная сила в этом сечении остается прежней Q_II=R_A=14 кН=const. Как видим, в эпюре Q в сечении С не происходит изменений.

Участок DВ. На этом участке удобнее поместить начало координат в точке В, тогда справа от произвольного сечении действует одна сила – реакция Rв, которая сдвигает правую часть балки вверх, и, поэтому, поперечная сила отрицательна.

Поперечная сила Q_III=-R_А=-6 кН=const. Как видим, на эпюре Q в сечении D имеется скачок, равный по величине приложенной в этом сечении силе F=20 кН.

Эпюра поперечных сил, построенная по вычисленным значениям, показана на (рис.20в).

В концевых сечениях поперечная сила равна опорным реакциям, под силой F на эпюре Q – скачок на величину силы F. Это свидетельствует о правильности построенной эпюры.

Построение эпюры М. Для построения эпюры изгибающих моментов границы участков оставляем прежними.

Участок АС. 0≤Z₁≤1. Для этого участка слева от сечения действует одна сила R_A, которая изгибает балку относительно мысленно закрепленного сечения выпуклостью вниз, следовательно изгибающий момент М_I=R_AZ₁=14Z_I – линейная функция.

При Z_I=0 M_I=0 – это в сечении А.

При Z_I=1 м М_I=14 1=14 кНм – это в сечении С в конце участка АС.

Участок СD. 1≤Z₂≤3. Для этого участка М_II=R_AZ₂-M – линейная функция. Сила R_A изгибает балку выпуклостью вниз, момент М – выпуклостью вверх.

При Z₂=1 M_II=14 1-30=-16 кНм

При Z₂=3 M_II=14 3-30=12 кНм.

Как видим на эпюре М в сечении С имеется скачок, равный по величине приложенному в этом сечении моменту М=30 кНм.

Участок DВ. 0≤Z₃≤2. Для этого участка M_III=RвZ₃ – линейная функция.

Сила Rв изгибает правую отсеченную часть балки выпуклостью вниз.

При Z₃=0 M_III=0

При Z₃=2_M M_III=6 2=12 кНм.

Выбор отсчета для участка DВ от правого конца балки с одной стороны упрощает расчет, с другой дает возможность осуществлять контроль правильности в определении изгибающего момента. В рассмотренном случае изгибающий момент определенный в сечении D на участке СD и DВ совпадают М =12кНм, что подтверждает правильность выполненных вычислений. По найденным значениям строим эпюру изгибающих моментов (рис.20г).

Из построенных эпюр видно, что опасным является сечение С, в котором возникает наибольший изгибающий момент Мmax=16 кН м.

Из условия прочности при изгибе Ϭ_max= ≤

Проверяем прочность балки.

Осевой момент сопротивления относительно оси х для двутавра №16 ГОСТ 8239-89 Wx=109 см³.

Наибольшее нормальное напряжение в опасном сечении

Ϭ_max=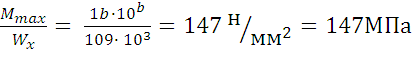

Что меньше предела текучести 180 МПа. Действительный коэффициент запаса прочности n=

Задача 13.

Для заданной балки (рис.21) требуется:

1. Построить эпюры поперечных сил и изгибающих моментов.

2. Из расчета на прочность подобрать двутавровое, круглое и прямоугольное сечения ( для прямоугольного сечения h:в=2),

если [Ϭ]=160 МПа, q=8 , F=26 кН, М=22 кНм, а=в=d=2 м с=4м.

1. Определение опорных реакций.

В балке возникают опорные реакции в т. А и В. R_A и Rв. Расчетная схема для балки представлена на рис.20б.

Составляем уравнение равновесия:

1. ΣМ_А(Fi)=M-q(c+d) + R_A+(а+в+с) =0

2. ΣМв(Fi)=- R_А(а+в+с)+F(a+в+c)+M+q с

Из уравнения (1):

Rв = 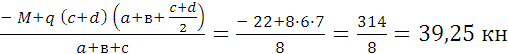кН

Rв=39,25 кН.

Из уравнения (2):

R_A= _кН

R_А=34,75 кН.

Проверяем правильность определенных реакций:

3. ΣFiy=R_A-F-q6+Rв=34,75-25-8 6+39,25=0 – реакции определены правильно.

2. Построение эпюры Q. Определяем расчетные участки. Границами участков являются точки приложения реакции R_A (т.А), сосредоточенного момента (т.Е), точка начала действия равномерно распределенной нагрузки (т. D), точка приложения реакции Rв (т.В), точка окончания действия равномерно распределенной нагрузки (т.К).

Имеем четыре участка (АС, СD, DВ, ВК).

Участок АС. 0≤Z₁≤2. Начало отсчета координаты Z выбрано в точке А. Слева от сечения действуют две силы R_А и F, поперечная сила в этом сечении Q_I=R_A-F=34,75-26=8,75 кН=const. Эпюра Q- прямая, параллельная оси Z.

Участок СD. 2≤Z₂≤4. Слева от сечения II-II приложены силы R_A, F и момент М, поперечная сила Q_II=R_A-F=34,75-26=8,75кН=const.

Эпюра Q- прямая, параллельная оси Z.

Участок ВК. 0≤Z₃≤2. отсчет абсциссы Z ведет от правого конца балки. На этом участке действует равномерно распределенная нагрузка интенсивностью q, направленная вниз и, поэтому, стремится сдвинуть правую часть балки вниз.

Поперечная сила в этом сечении Q_III=qZ₃ – линейная зависимость, эпюра Q – наклонная прямая линия.

При Z=0 Q_III=0

При Z=2 Q_III=8 2=16 кН.

Участок DВ. 2≤Z₄≤6. Поперечная сила на этом участке Q_IV=qZ₄-Rв.

Из этого выражения видно, что поперечная сила изменяется по закону прямой линии.

При Z=2 Q_IV=8 2-39,25=-23,25 кН.

При Z=6 Q_IV=8 6-39,25=8,75 кН.

По найденным ординатам строим эпюру поперечных сил рис.20в.

3. Построение эпюры изгибающего момента М.

Изгибающие моменты в характерных сечениях определяем по участкам.

Участок АС. 0≤Z₁≤2.

М_I=R_AZ₁-FZ₁- линейная функция, эпюра М – наклонная прямая линия.

При Z₁=0 М_I=0

При Z₁=2 М_I=34,75 2-26 2=17,6 кН м.

Участок СD. 2≤Z₂≤4.

М_II=R_AZ₂-FZ₂-M – линейная функция, эпюра М наклонная прямая линия.

При Z₂=2 М_II=34,75 2-26 2-22=-4,5 кН м.

При Z₂=4 М_II=34,75 4-26 4-22=13 кН м.

Участок ВД. 0≤Z₃≤2.

М_III=-qz₃ - квадратичная функция, эпюра М – парабола.

При Z₃=0 М_III=0

При Z₃=2 М_III=

Участок DВ. 2≤Z₄≤6.

М_IV= - квадратичная функция, эпюра М – парабола.

При Z₄=2 М_IV =- 16 кНм

При Z₄=6 М_IV = 13 кНм

z

y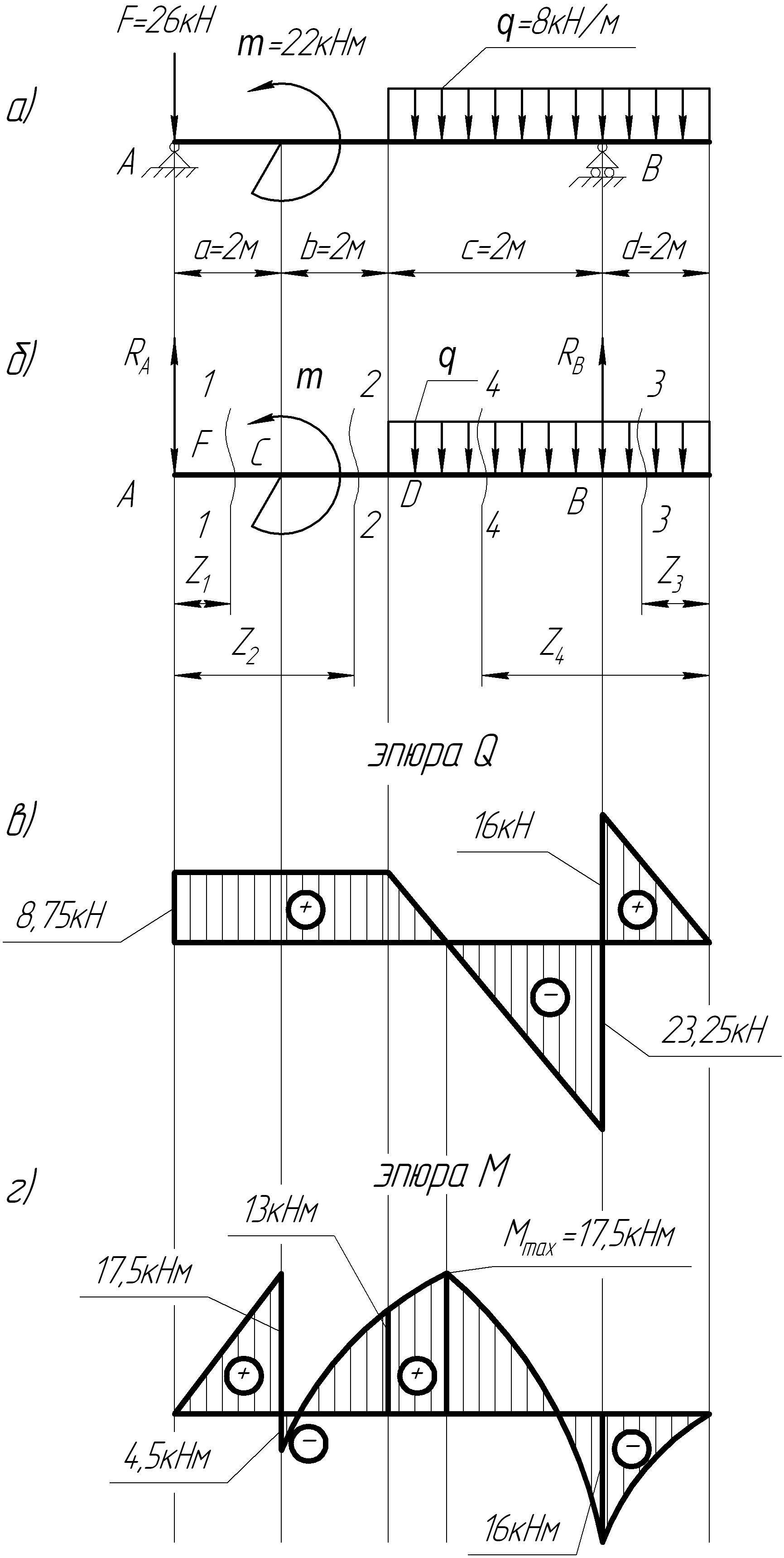

Рис.21

По полученным значениям построена эпюра изгибающих моментов рис.20г. Так как на участке DВ поперечная сила обращается в нуль, то в точке, где Q=0, изгибающий момент принимает экстремальное значение. В соответствии с дифференциальной зависимостью находим производную от М_IV.

Откуда Z₄= ≈5 м;

Определяем

M_IV,Z4=5=

Таким образом Мmax=17,75 кН м.

4.Размеры поперечного сечения определяем из условия прочности при изгибе

Ϭ_max= ≤[Ϭ]

Определяем осевой момент сопротивления площади сечения относительно оси х.

Wx = мм³=110,9 см³.

Wx=110,9 см³.

Размеры поперечного сечения определяем в трех вариантах:

а) сечение двутавровое, размеры поперечного сечения определяем в соответствии с ГОСТ 8239-89, ближайшее значение Wx=109см³, что соответствует двутавру №16.

б) сечение круглое, осевой момент сопротивления для которого определяется по формуле:

Wx=0,1d³.

Откуда d=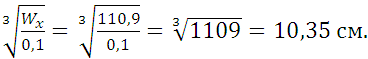

Принимаем d=104 мм.

в) сечение прямоугольник с отношением сторон h:в=2

Осевой момент сопротивления для прямоугольного сечения определяется по формуле W_x =

Выразим высоту сечения h через ширину в h=2в и подставим в формулу осевого момента сопротивления: W_x =

Отсюда в=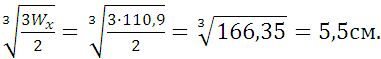

в=5,5 см, h=2в=2 5,5=11см. h=11 см.

Принимаем в=60 мм; h=120 мм.

Задача 14.

Определить из условия прочности допускаемую нагрузку , которую можно приложить к балке с коробчатым поперечным сечением,

если [Ϭ]=160 МПа, а=1м (рис.22).

Решение.

Определение опорных реакций, составление уравнений поперечных сил и изгибающих моментов и вычисление внутренних силовых факторов удобнее выполнять в общем виде, т.е. выражать через q и а и лишь на завершающем этапе подставлять значения а.

Составляем уравнения равновесия для определения опорных реакций. Расчетная схема представлена на (рис.22б).

1. ΣМ_А(Fi)=М-q 4a 3a-F 6a+Rв 5а=0 Rв=3,2qа.

2. ΣМв(Fi)=-R_А 5а+М+q 4а 2а-F а=0 R_А=1,8qa.

Проверка: ΣF_iy=R_A-q 4a-F=1,8qa-4qa-3,2qa=0.

Построение эпюры Q. Расчетная схема имеет три участка (АС, СВ, ВD).

Участок АС. Q_I=R_A=1,8qa=const 0≤Z₁≤a

Участок СВ. Q_II=R_A-q(Z₂-a) – уравнение наклонной прямой линии. а≤Z₂≤5a

При Z₂=a, Q_II=1,8qa

При Z₂=5a Q_II=1,8qa-q 4a=-2,2qa.

Участок ВD. Q_III=F=qa=const 0≤Z₃≤a

Строим эпюру поперечных сил (рис.22в).

Проверяем правильность построенной эпюры Q. На концевых сечениях балки поперечная сила соответственно равна реакции R_A=1,8qa и сосредоточенной силе F=qa, в точке «В» происходит скачок на величину силы Rв=3,2qa.

Построение эпюры М. Изгибающий момент в I и III сечении изменяется по линейному закону, так как отсутствует на участке АС и ВD равномерно распределенная нагрузка. На участке СВ эпюра М представляет собой параболу, т.к. на нем приложена равномерно распределенная нагрузка. Вычислим значения М на этих участках.

Участок АС. М_I=-M+R_AZ₁ 0≤Z₁≤a

При Z₁=0 M_I=-M=-2qa²

При Z₁=a M_I=-2qa2+1,8qa a=-0,2qa².

Участок СВ. а≤Z₂≤5а

М_II=-M+R_AZ₂-q(Z₂-a)

При Z₂=а M_II=-2 qa²+1,8qa2=-0,2qa²

При Z₂=5a M_II=-2qa²+1,8qa 5a-q =-2qa²+9qa²-8qa²=-qa²

Так как на этом участке на эпюре Q находится точка, в которой Q=0, то в этой точке изгибающий момент принимает экстремальное значение, которое можно определить, использовав дифференциальную зависимость

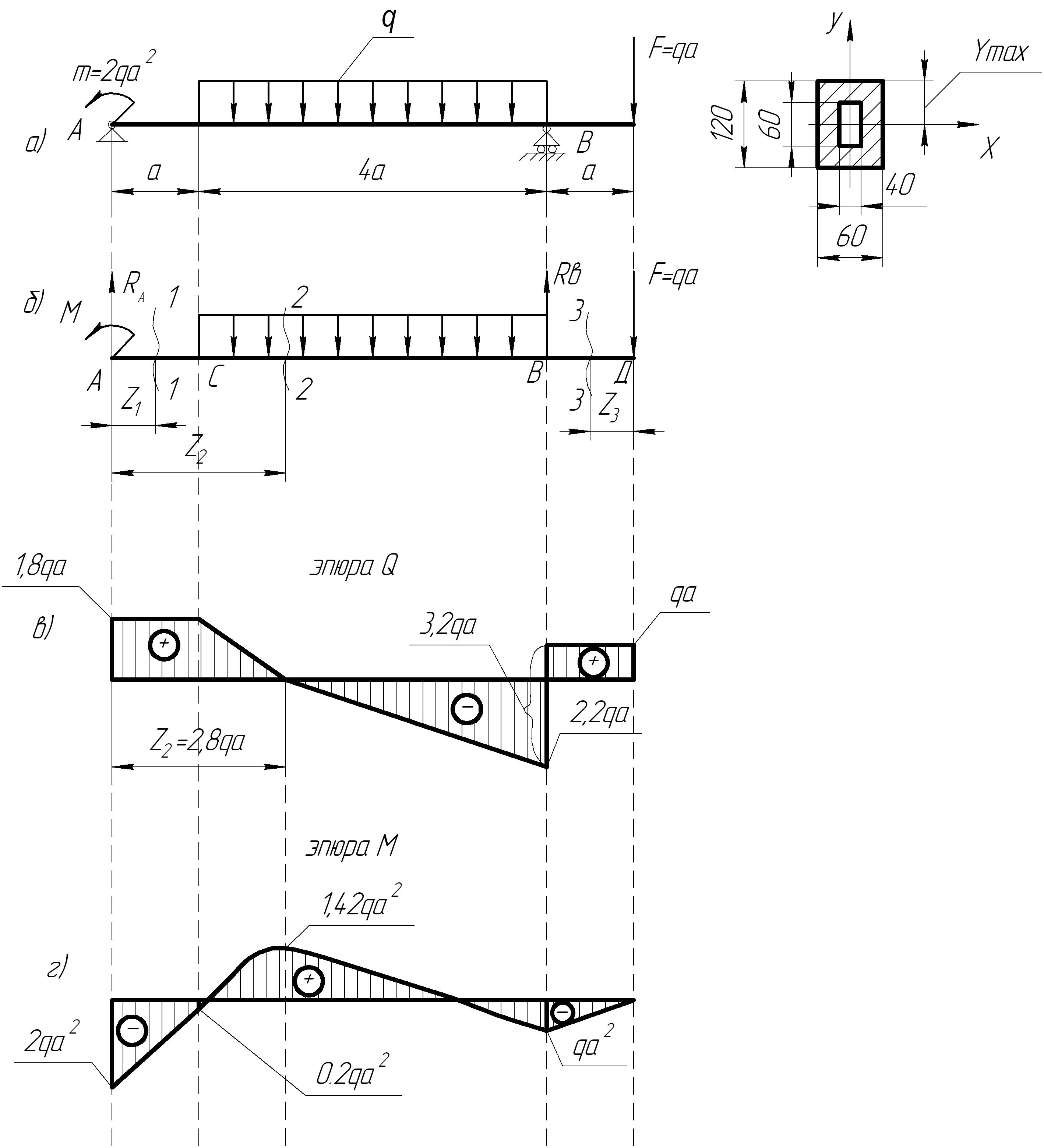
рис.22

Находим

Откуда Z₂=

При Z₂=2,8а М_II=-2qa2+1,8qa 2,8a- =-2qa²+5,04qa²- 1,62=1,42qa².

По найденным значениям строим эпюру изгибающих моментов (рис.22г).

Опасное сечение находится в точке А, где ׀М_max׀=2qa².

Допускаемую нагрузку [q] определяем из условия прочности при изгибе

Ϭ_max= ≈[Ϭ]

Из правой части расчетного уравнения М_max=Wx[Ϭ]

Подставляя значения М_max=2qa², получаем 2qa²=Wx[Ϭ],

откуда [q] =

Определяем осевой момент сопротивления коробчатого сечения

Wx= , где Jx=

_max= 6 см.

Осевой момент сопротивления Wx= см³.

Допускаемая нагрузка [q]=

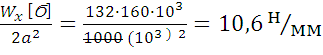
[q]=10,6н/мм=10600н/м≈1,06