2. Построение эпюры q.

Выбираем сечение I-I на расстоянии от свободного конца. Сил, перпендикулярных оси балки, нет; поперечная сила Q по всей длине балки равна нулю

Q_I=0 0≤ ≤ ℓ

Эпюра Q представлена на (рис. 13б).

3. Построение эпюры м.

Мысленно отсекаем правую часть балки, определяем изгибающий момент в сечении I-I. На правую часть действует только сосредоточенный момент М, который изгибает отсеченную часть балки выпуклостью вверх (рис.14),

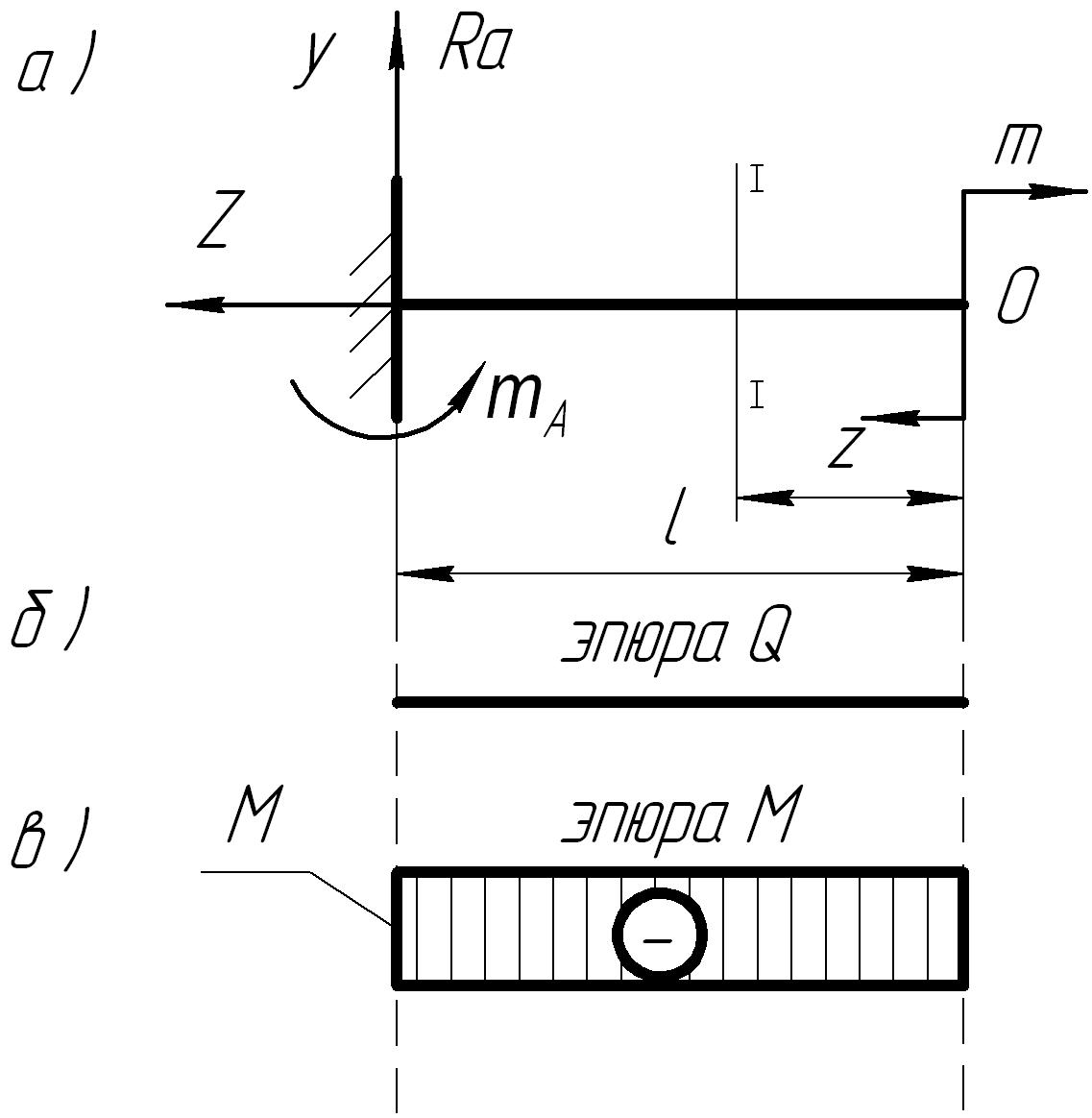
Рис.13

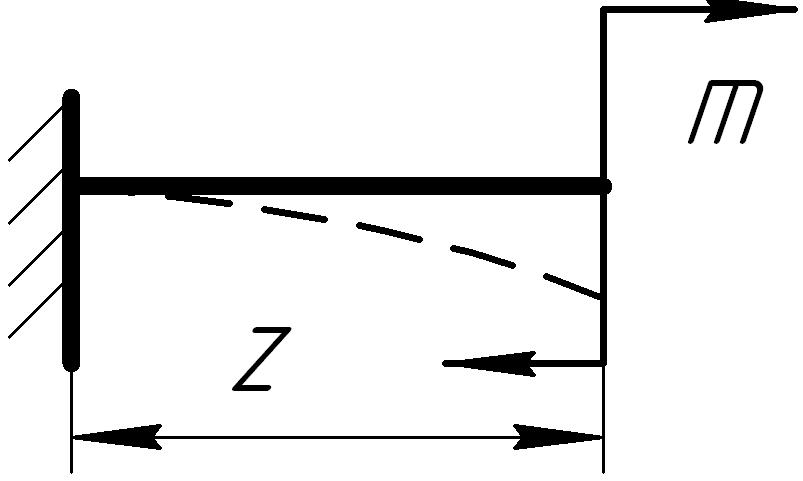
Рис. 14

Изгибающий момент M_I=-M. Это выражение представляет собой уравнение прямой линии, параллельной оси х. Относительно любого сечения х момент внешней пары одинаков, т.е. М( )=-М 0≤ ≤ ℓ.

Это значение откладываем в некотором масштабе вниз от линии отсчета и строим эпюру изгибающих моментов, штрихуем ее перпендикулярно оси балки и указываем знак в кружке, который располагаем в середине балки (рис. 13).

Задача7

Построить эпюру поперечных сил и изгибающих моментов для балки защемленным одним концом и нагруженной равномерно распределенной нагрузкой по всей длине (рис. 15а).

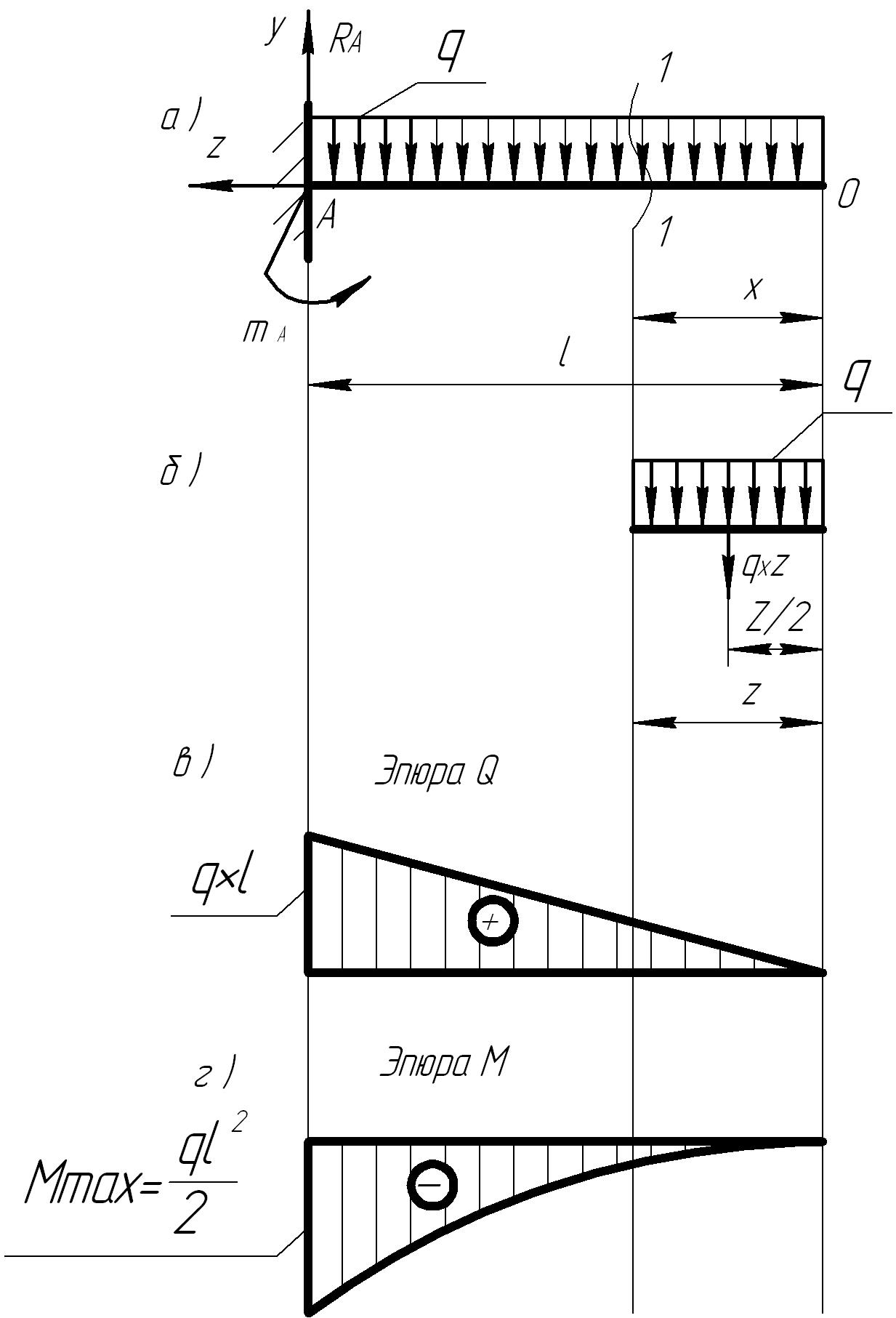
Рис.15

Решение.

1. Определение опорных реакций.

В заделке возникает вертикальная реакция R_A и реактивный момент m_A. Составляем уравнение равновесия в форме:

1. ΣFiy=R_А-qℓ=0; R_A=qℓ

2. ΣM_A(Fi)=m_A-q ℓ

m_A =

2. Построение эпюры q.

На произвольном расстоянии от свободного конца балки проводим сечение I-I, отбрасывая левую часть балки и рассматривает равновесие правой (рис15б). Поперечная сила в сечении I-I равна алгебраической сумме всех внешних сил, действующих справа от рассматриваемого сечения. На правую часть балки действует равномерно распределенная нагрузка q на длине эта нагрузка q сдвигает правую часть балки вниз, приложена посередине отсеченной части, поэтому она положительна.

Следовательно Q_I=q , где изменяется в пределах от 0≤ ≤ℓ.

Из этого выражения видно, что поперечная сила изменяется по закону наклонной прямой линии.

Q_{I ,=0}=0; Q_{I =ℓ} =qℓ

Эпюра Q показана на (рис15в).

3. Построение эпюры М. На произвольном расстоянии от свободного конца в сечении I-I изгибающий момент равен алгебраической сумме моментов всех внешних сил, действующих справа от рассматриваемого сечения.

В сечении с координатой равнодействующая равна q , плечо ее равно Равномерно распределенная нагрузка на участке длиной z , относительно центра тяжести сечения дает момент

М_I=-q = - , где z изменяется 0≤ ≤ ℓ. Момент МI – отрицателен, т.к. правая часть балки изгибается выпуклостью вверх. С увеличением момент алгебраически возрастает, причем закон его изменения выражается квадратной параболой (абсцисса входит во второй степени). Вершина параболы соответствует свободному концу при =0; М_I=0.

Наибольшее по абсолютной величине значение изгибающего момента соответствует заделке, для которой М_{I =ℓ} = -

Для графического построения параболы необходимо вычислить несколько промежуточных значений при = , = ; =

Эпюра М представлена на (рис. 15г).

Задача 8

Построить эпюры поперечных сил и изгибающих моментов для балки (рис) защемленной одним концом и нагруженной сосредоточенной силой F=12 кН равномерно распределенной нагрузкой q=20кн/м и сосредоточенным моментов М=30 кНм.

Решение.

1. Определение опорных реакций из уравнений равновесия.

1. ΣFiy=R_А-q3-F=0; R_А=q3+F=20x3+12=72 кН

2. ΣM_А(F_i)=m_А-q 3 2,5-F4-M=0;

m_А=q 3 2,5+F 4+M=20 3 2,5+12 4+30=150+78=228 кНм.

2. Построение эпюры поперечных сил Q. Выбираем характерные сечения балки I-I, II-II, III-III, отсчитывая от свободного конца балки.

I-й участок балки 0≤ ₁≤2

Поперечная сила Q_I=0, так как справа от сечения алгебраическая сумма проекции внешних сил равна нулю. На этом участке эпюра Q есть прямая, совпадающая с осью балки.

II участок балки 2≤ ₂≤5

Поперечная сила Q_II=F+q( ₂-5)

Q_{II, 2=2}=F=12 кН Q_{II, 2=5}=F+q(5-2)=12+20 3=72кН

Так как уравнение Q_II есть линейная функция, то эпюра Q на этом участке представляет собой наклонную прямую линию.

III участок

Поперечная сила Q_III=F+q3=12+60=72кН

Эпюра поперечной силы – прямая параллельная оси . эпюра Q построена на (рис16 б).