4. Поперечный изгиб.
4.1. Основные положения и расчетные формулы.
Изгибом называется такая деформация бруса, при которой его ось и продольные волокна искривляются под действием сил, перпендикулярных к его оси, или пар сил, лежащих в плоскостях, проходящих через эту ось (рис.7).
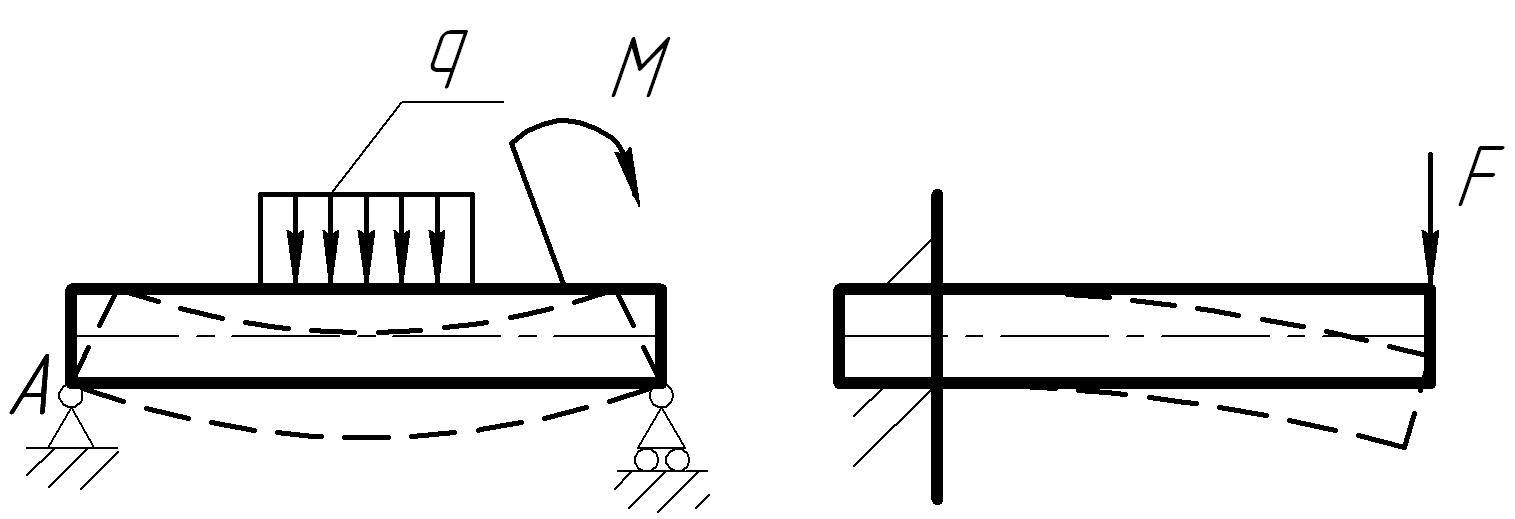
Рис.7
Изгиб, при котором в поперечных сечениях возникает только изгибающий момент, называется чистым изгибом.
В общем случае изгиб сопровождается одновременно изгибающим моментом М и поперечной силой Q. Такой изгиб называется поперечным.
Брус, работающий на изгиб, обычно называют балкой. Балка имеет опорные закрепления, от устройства которых зависят опорные реакции. Различают три вида опор: неподвижная шарнирная, подвижная шарнирная и жесткая заделка, или защемление. Реакции опор определяют из уравнений равновесия.
Используя метод сечений, определяют поперечную силу и изгибающий момент в сечении балки. Поперечная сила Q в сечении численно равна алгебраической сумме внешних (поперечно направленных) сил, приложенных по одну сторону от сечения.
Изгибающий момент М в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторон от сечения относительно его центра тяжести.
Правило знаков.
При вычислении поперечной силы в некотором сечении внешние силы, расположенные слева от сечения и направленные вверх или расположенные справа от сечения и направленные вниз, следует считать положительными и наоборот отрицательными (рис.8а).
Изгибающий момент считают положительным, если внешние силы, приложенные по одну сторону от сечения, изгибают балку в области этого сечения выпуклостью вниз (рис.8б).
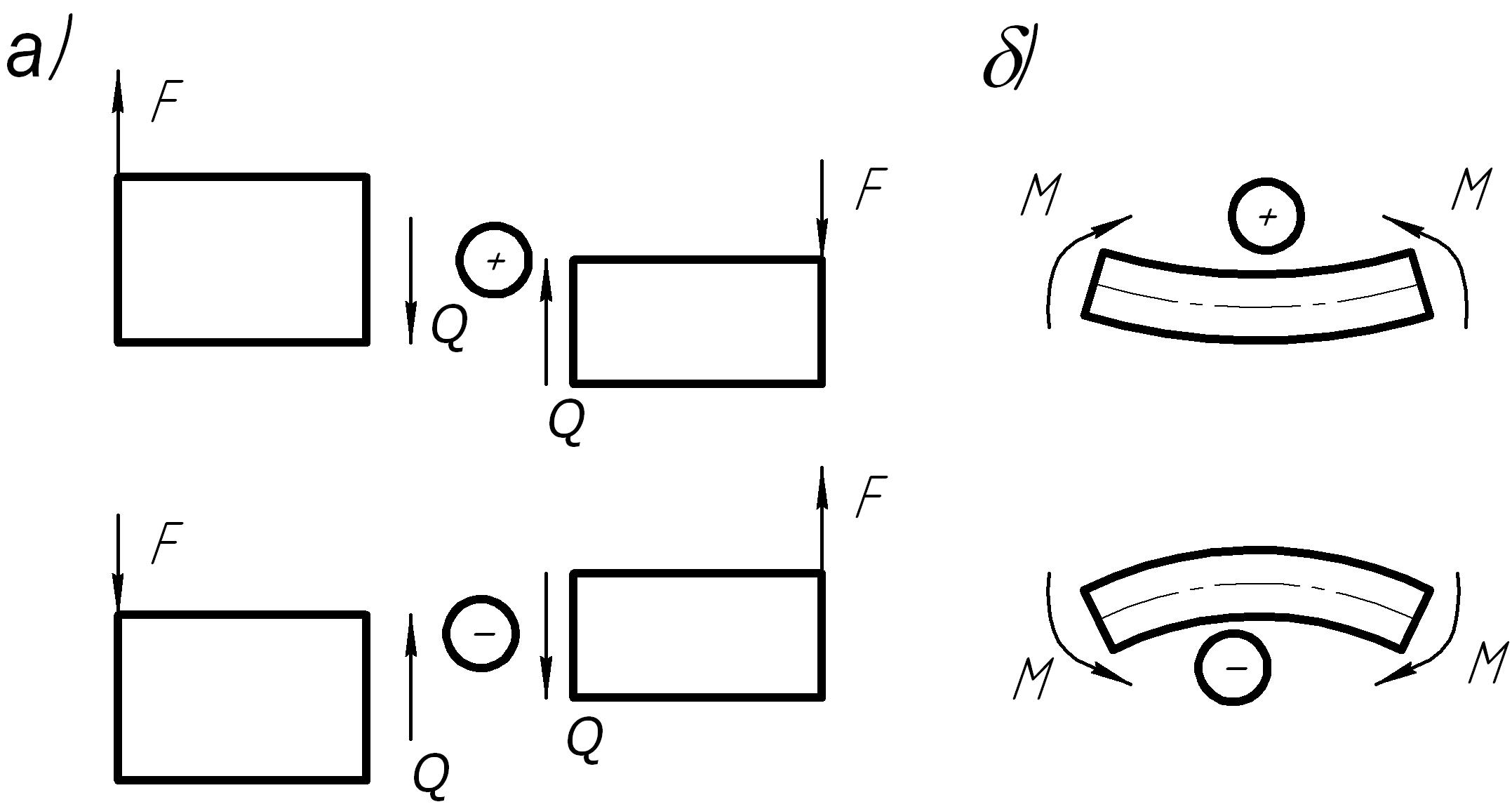
Рис.8
При определении знака изгибающего момента мысленно закрепляют сечение отсеченной части балки и отбрасывают другие опоры, заменив их действие реакциями связей. Положительными считают моменты внешних сил, изгибающие полученную консольную балку вверх независимо от их расположения и отрицательными, изгибающими балку вниз (рис.9 а и б)
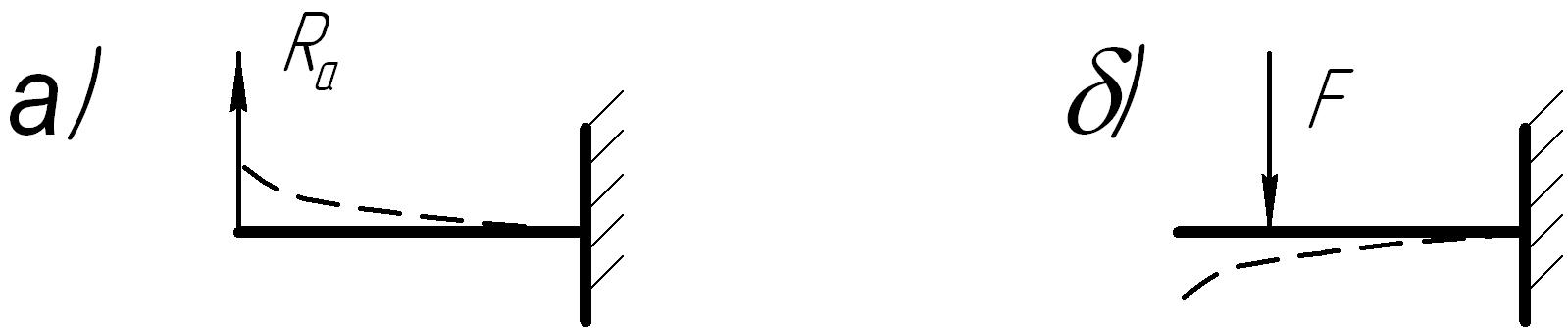
рис.9
Изменение поперечной силы и изгибающего момента по длине балки изображают графически, что придает расчету наглядность и позволяет быстрее находить опасные сечения и облегчает подбор размеров сечений балки.
Эпюра поперечной силы есть график, ордината которого в каждой точке выражает в масштабе величину поперечной силы в данном сечении. Положительные значения поперечной силы откладываются вверх от оси, отрицательные – вниз.
Эпюра изгибающего момент есть график, ордината которой в каждой точке выражает в масштабе величину изгибающего момента в данном сечении. Положительные ординаты опор откладывают вверх, отрицательные вниз.
Между М, Q и интенсивностью распределенной нагрузки q существует зависимость:
которые используются при проверке правильности построения эпюр поперечных сил и изгибающих моментов.
Во всех точках
поперечного сечения балки при поперечном
изгибе возникают Ϭ
– нормальные и Շ
– касательные напряжения. На (рис.10) эти
напряжения показаны в точках, отстоящих
на расстоянии у от оси х и определяются
по формулам:
Ϭ=
; Շ=
σ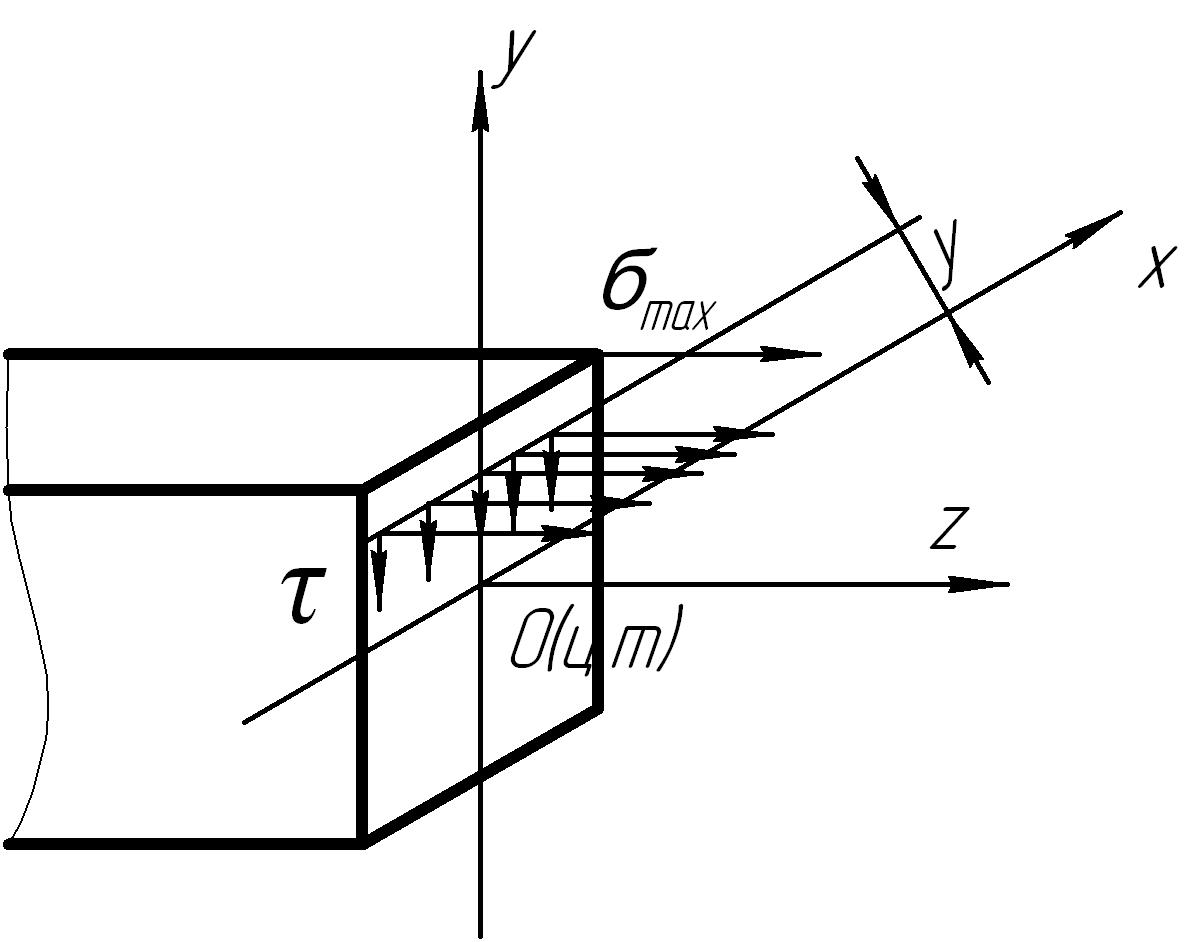
Рис. 10
С увеличением координаты у нормальные напряжения увеличиваются и в наиболее удаленных от нейтральной оси достигают наибольшего значения:
Ϭ
max=
В расчетах
используется специальная геометрическая
характеристика – осевой момент
сопротивления сечения при изгибе:
Wx=
Тогда Ϭmax=
Касательные
напряжения по сравнению с нормальными
пренебрежимо малы и при расчете на
прочность в большинстве случаев не
учитываются.
Условия прочности
при изгибе имеет следующий вид: Ϭmax
где Ϭ max берется по абсолютной величине. Подставляя вместо Ϭ max его значение, получаем условие прочности в следующей форме:
Ϭmax
= 