ББК

Печатается по решению Учебно-методического Совета НТГСПА

(протокол № ____ от ______________ 2007 г.)

РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ. Выпуск 2. Кручение. Поперечный и продольный изгиб. Сложное сопротивление бруса. Методическое пособие для самостоятельной работы студентов/Авт.-сост. В.А.Чумаков. – Нижний Тагил, 2007. - с.

Рецензенты:

В.К. Колесников, к.п.н, доцент кафедры технологии обработки материалов НТГСПА.

Р.А. Дмитриева, доцент кафедры теории и методики технологического образования НТГСПА.

Учебное пособие содержит минимально необходимый теоретический материал по темам "Кручение. Поперечный и продольный изгиб. Сложное сопротивление бруса", который может потребоваться при прочностных расчётах. Акцент сделан на методические рекомендации, дающие возможность решать типовые задачи, которые даны с подробными решениями, что позволяет использовать пособие в процессе самостоятельной работы над курсом "Сопротивление материалов".

Для повышения обучающих возможностей пособия и обеспечения удобства в освоении новой информации в начале пособия даны все имеющиеся обозначения, а в конце содержится материал по геометрическим характеристикам плоских сечений и сортаменту прокатных профилей.

Пособие предназначено для студентов дневного и заочного отделений факультета технологического образования и может использоваться в технических колледжах.

Редактор

Корректор

Компьютерная верстка

Подписано в печать . Формат 60×84 1/16. Бумага для множительных аппаратов. Гарнитура «Таймс». Печать офсетная (на ризографе). Усл. печ. л. . Уч.-изд. л.

Тираж экз. Заказ №

Оригинал-макет изготовлен в РИО НТГСПА. Отдел издательских и множительных систем НТГСПА.

Адрес: 622031, Нижний Тагил, ул. Красногвардейская, 57.

1. Перечень основных обозначений величин и их наиболее употребляемые единицы

A – площадь поперечного сечения, м²;

E – модуль продольной упругости, МПа;

F, P – сила (сосредоточенная), кН;

G – модуль сдвига, МПа;

J – момент инерции сечения, м⁴;

J_x, J_y – осевые моменты инерции, м⁴;

J_xy – центробежный момент инерции, м⁴;

J_p – полярный момент инерции, м⁴;

M – изгибающий момент, кН·м;

Mкр – крутящий момент, кНм;

N – продольная сила, кН;

Q – поперечная сила, кН;

[σ] – допускаемое напряжение, МПа;

S – статический момент сечения, м³;

W – момент сопротивления сечения, м³;

X – реакция в отброшенной связи, кН; кН·м;

b, d, h – ширина, диаметр, высота сечения, м;

i – радиус инерции сечения, м;

ℓ– длина стержня, балки, м;

m – сосредоточенный момент; пара сил, кН·м;

q – интенсивность распределенной силы, кН/м;

v – перемещение в направлении оси y, мм;

w – перемещение в направлении оси z, мм;

γ – удельный вес, кН/м³;

Δ, δ – перемещение линейное, мм;

ε – деформация;

λ – гибкость стержня;

μ – коэффициент приведения длины стержня;

ν – коэффициент Пуассона;

σ – нормальное напряжение, МПа;

τ – касательное напряжение, МПа;

φ – коэффициент продольного изгиба;

ө - угол поворота поперечного сечения, рад.

1. Введение.

Сопротивление материалов – фундаментальная дисциплина физико – математического цикла – развивает не только общеинженерную, но и общенаучную базу учителя технологии. Ведущее место в курсе отводится освоению методов расчета элементов конструкций. Но решение задач по сопротивлению материалов вызывает у студентов определенные трудности.

Методическое пособие даст возможность преодолеть эти трудности, лучше организовать самостоятельную работу как на практических занятиях, так и при выполнении расчетно – графических заданий. Особое внимание в пособии уделено подробному анализу решения задач по теме поперечный изгиб, имеющие наибольшее практическое применение в специальных дисциплинах.

Каждый новый тип задач объясняется на конкретном примере с подробными пояснениями. В пособии приводится минимум теории, который необходим для решения задач, сводка основных формул и справочные данные для геометрических характеристик плоских сечений и коэффицентов продольного изгиба.

Знания и навыки, полученные студентами при решении задач по темам "Кручение", "Поперечный и продольный изгиб", сложное сопротивление найдут применение при выполнении выпускных квалификационных работ.

3. Кручение

0. 3.1. Краткие теоретические сведения о кручении.

Брус испытывает кручение, когда внутренние усилия в его поперечных сечениях приводятся к парам сил, вызывающим поворот сечений в плоскостях перпендикулярных к продольной оси бруса.

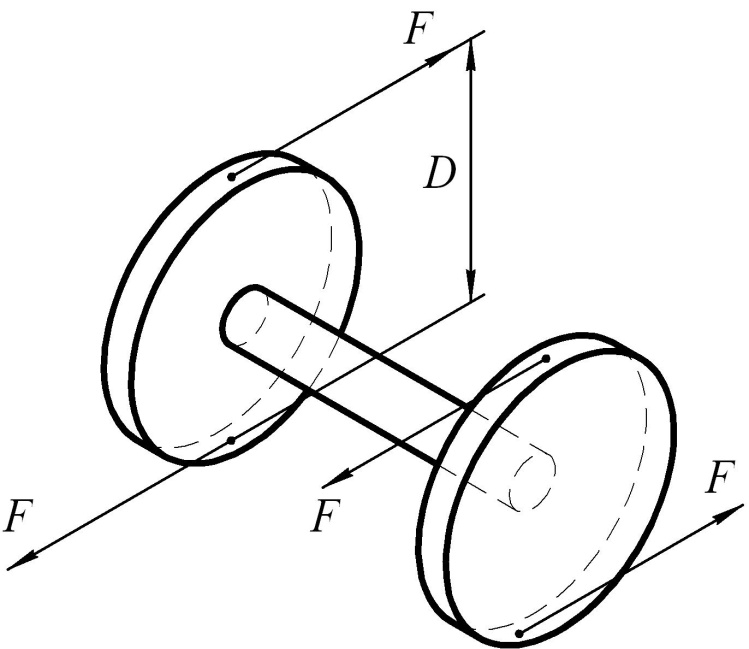
Рис.1

Брусья, работающие на кручение, называются валами. Момент внешних пар, являющихся нагрузками для валов передаются через зубчатые колеса, шкивы, ременные передачи и называются скручивающими моментами. На (рис.1.) изображен круглый вал АВ, на который действует два скручивающих момента, приложенных по его концам. Моменты равны по величине и противоположны по направлению. На вал могут действовать несколько скручивающих моментов. Если задана величина усилия F, действующая на зуб шестерни или обод шкива, то скручивающий момент определяется как произведение действующей силы на плечо (где D - диаметр делительной окружности зубчатого колеса или диаметр шкива). , в случае, если задана передаваемая мощность N в квт и угловая скорость в радианах в секунду, то скручивающий момент определяется

по формуле , где , n – число оборотов в минуту вала. Таким образом, кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент M_кр.

Крутящим моментом в поперечном сечении бруса называется результирующий момент относительно геометрической оси бруса внутренних упругих касательных сил, возникающих в данном сечении. Для определения крутящего момента M_кр используется метод сечений.

Брус мысленно разрезают по рассматриваемому сечению на две части, одну из которых отбрасывают. К оставшейся части прикладывают крутящий момент, уравновешивающий отброшенную, и из условия равновесия находят искомый крутящий момент (рис.2.)

Р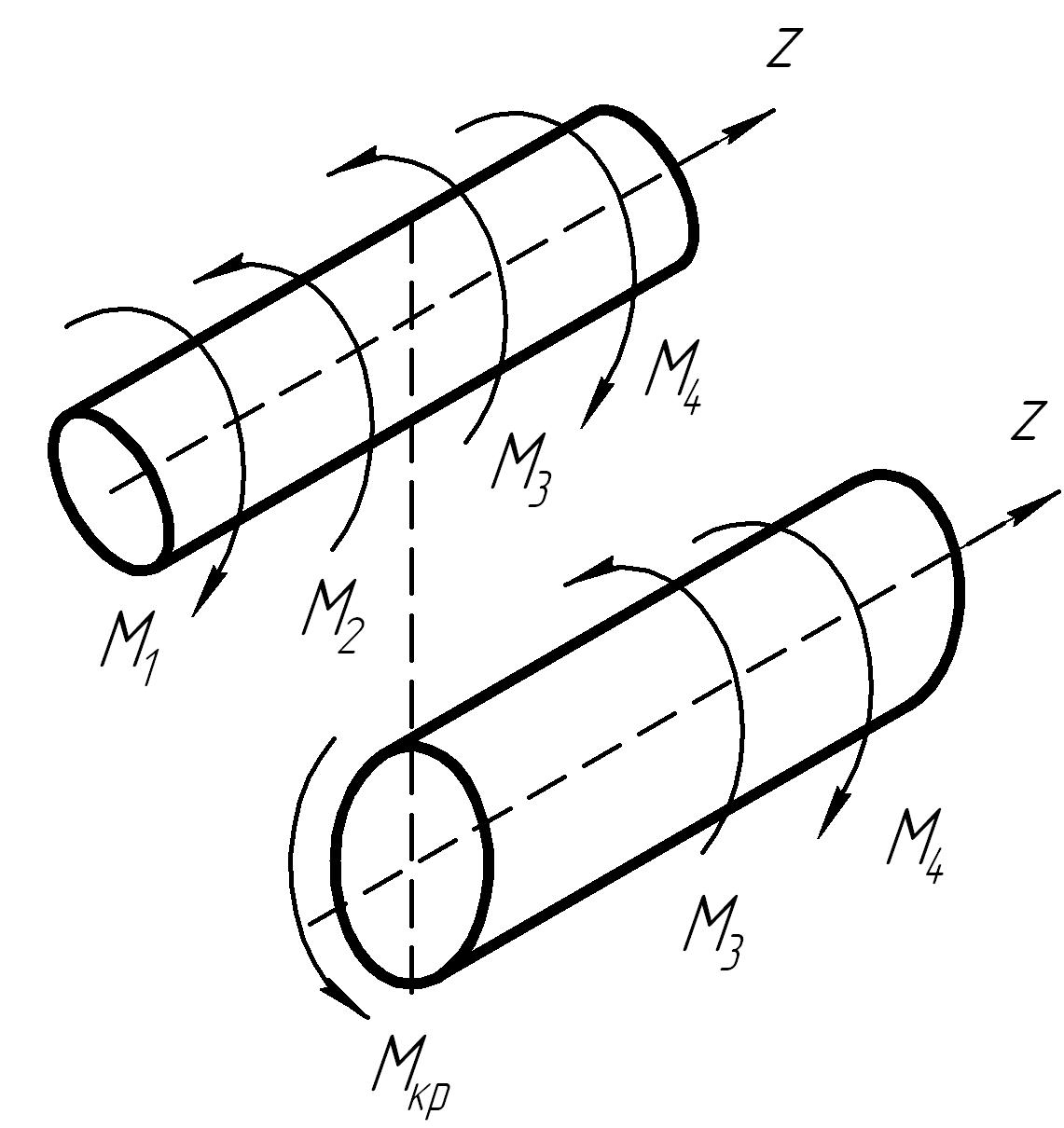

Рис. 2

Величина крутящего момента, возникающего в поперечном сечении бруса, равна алгебраической сумме скручивающих моментов внешних пар сил, действующих по одну сторону от сечения , где - алгебраическая сумма моментов сосредоточенных скручивающих моментов, расположенных с одной стороны от сечения, перпендикулярных продольной оси бруса. Условимся считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке. Соответствующий внешний момент направлен против часовой стрелки (рис.3.)

Рис.3

Если к брусу приложено несколько скручивающих моментов (рис.2), то крутящий момент будет оставаться постоянным в пределах каждого участка между смежными скручивающими моментами и меняется скачкообразно в сечениях, где эти моменты приложены. График, показывающий закон изменения величины крутящего момента по длине бруса, называется эпюрой крутящих моментов.

Следует иметь ввиду, что при установившемся равномерном вращении вала алгебраическая сумма скручивающих моментов, приложенных к нему, должна быть равна нулю.

В поперечных сечениях вала при кручении возникают только касательные напряжения . В любой части поперечного сечения вала на расстоянии ρ от центра тяжести сечения они определяются по формуле

τ _ρ = ;

Максимальные касательные напряжения возникают на контуре (рис.4):

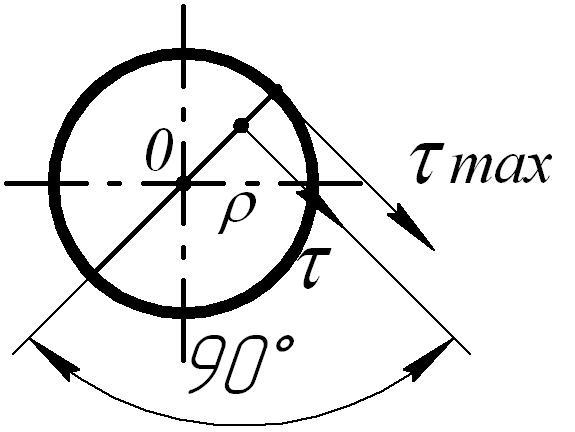
Рис.4

;

где - полярный момент инерции;

W_p – полярный момент сопротивления.

Условие прочности имеет вид:

.

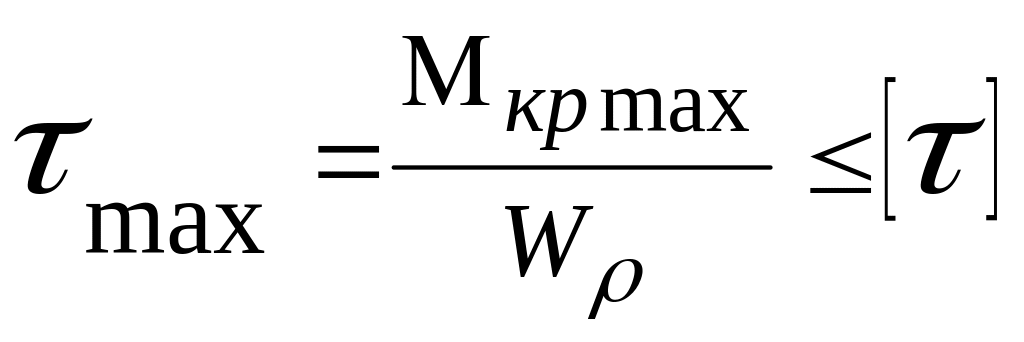Допускаемое напряжение при кручении :

для хрупких материалов:

;

для пластичных материалов:

.

Оценку деформации вала при кручении определяет угол закручивания . Угол закручивания определяют по закону Гука:

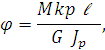
где ℓ - длина участка;

- жесткость сечения вала при кручении: - измеряется в радианах.

Относительный угол закручивания

.

Условие жесткости , где - допускаемый угол закручивания, или .

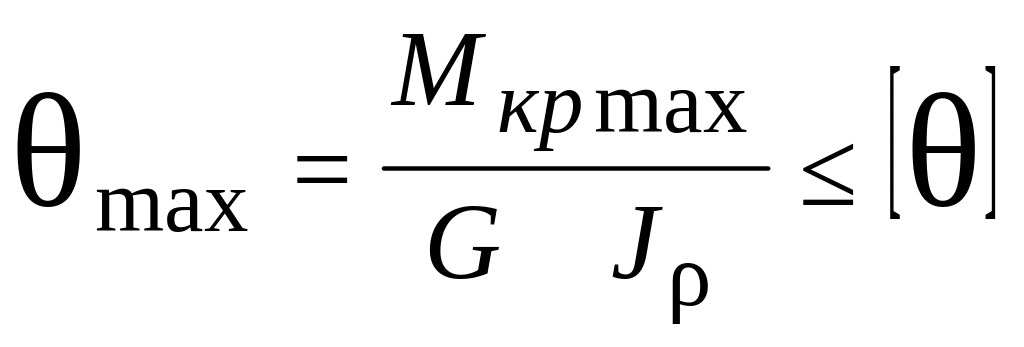Если наибольший относительный угол закручивания задан в градусах, то условие жесткости принимает вид:

.

Допускаемый относительный угол закручивания принимается для разных конструкций валов и различных видов нагрузки в диапазоне (0,1-2,1) градусов (максимально до 5^о) на один погонный метр или 0,00175-0,035 радиан на один метр длины вала.

Условие прочности , как и любое условие прочности, позволяет решать три типа задач.

1.Проверка прочности (проверочный расчет). Известен наибольший крутящий момент и диаметр поперечного сечения вала (т.е полярный момент сопротивления). Расчет производится непосредственно по формуле условия прочности.

2. Подбор сечения (проектный расчет). По найденному наибольшему крутящему моменту и заданному допускаемому напряжению необходимо расчетным путем определить D – диаметр поперечного сечения вала, воспринимающей заданную внешнюю нагрузку без разрушения.

Из условия прочности определяют полярный момент сопротивления Wp= . Так как , то 0,2 D³ = , отсюда требуемый диаметр

D=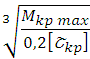

3. Определение допускаемого крутящего момента по известному диаметру поперечного сечения вала (полярному моменту сопротивления) и заданному допускаемому напряжению:

M_кр.доп. .

Условие жесткости при кручении позволяет производить три вида расчетов на жесткость:

1. Проверка жесткости (проверочный расчет)

.

2. Подбор сечения (проектный расчет). Из условия жесткости

определяется полярный момент инерции

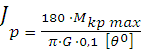откуда требуемый диаметр

D =

3. Определение допускаемого крутящего момента по известной жесткости и заданному допускаемому углу закручивания:

;

Для оценки прочности и жесткости валов при кручении применяются следующие геометрические характеристики плоских сечений:

площадь кругового сечения диаметра D;

полярный момент инерции круга;

полярный момент сопротивления кругового сечения;

- площадь кольцевого сечения с наружным диаметром D и внутренним d, где ;

полярный момент инерции для сечения кольцевого профиля;

полярный момент сопротивления кольцевого профиля.