2.2. Примеры расчета на прочность и жесткость.

Задача 2.

Для заданной стержневой системы (рис. 3).

1. Определить усилия в стержнях;

2. Вычислить напряжения в поперечных сечениях стрежней.

3. Проверить прочность стержней, указав на сколько (в процентах) каждый из стержней недогружен или перегружен. Материал стержней сталь Ст.3, имеющая предел текучести σ_т = 240МПа, требуемый коэффициент запаса по отношению к пределу текучести [n_т] = 1,5.

К решению подобного типа задач рекомендуется приступать, повторив раздел "статики" составление и решение уравнений равновесия плоской системы произвольно расположенных сил и иметь четкое представление об определении допускаемых напряжений и расчетах на прочность при растяжении и сжатии.

В первую очередь освобождают тело от связей и заменяют их действие на него реакциями связей, которые равны по величине продольным силам. Составляя уравнения равновесия для внешних сил, действующих на систему, и реакций связей, определяют продольные силы в поперечных сечениях бруса.

Площади поперечных сечений стержней определяют для нестандартных профилей, по формулам:

- круглое поперечное сечение , где d – диаметр стержня,

- прямоугольное сечение А = вh, где в и h стороны прямоугольного сечения.

Для профилей стандартного проката (равнополочные и неравнополочные угловые профили, швеллеры и двутавры) площади поперечных сечений определяются по таблицам ГОСТ.

Допускаемое напряжение определяется отношением предела текучести к требуемому (заданному) коэффициенту запаса [σ] = σ_т/[n_т].

Решение.

Применяем метод сечений и рассматриваем равновесие стержневой системы под действием сил F₁, F₂ и продольных сил N₁, N₂, N₃. Начало координат возьмем в точке В, направим ось х по оси балки АВ, а ось y вертикально вверх. Спроектировать все силы на ось Вх, получим

ΣF_ix = -N₂ sinα + N₃ sinβ = 0 (1)

Спроектировав все силы на ось Вх, получим

ΣF_iy = N₂ cosα + N₃ cosβ + N₁ – F₁ – F₂ = 0 (2)

Взяв сумму моментов всех сил относительно точки В (в которой пересекаются две неизвестные силы N₂ и N₃), получим

ΣМ_В(F_i) = -N₁·4а + F₁·3а + F₂·а = 0, (3)

откуда ; N₁ = 11 кН

Решим совместно уравнения (1) и (2). Из уравнения (1)

-N₂ sin 60⁰ + N₃ cos 45⁰ = 0

выражаем ; (4)

поставим N₂ в уравнение (2)

; 1,12N₃ = 9

N₃ = кН; N₃ = 8,04 кН

Подставив N₃ в уравнение (4), получим

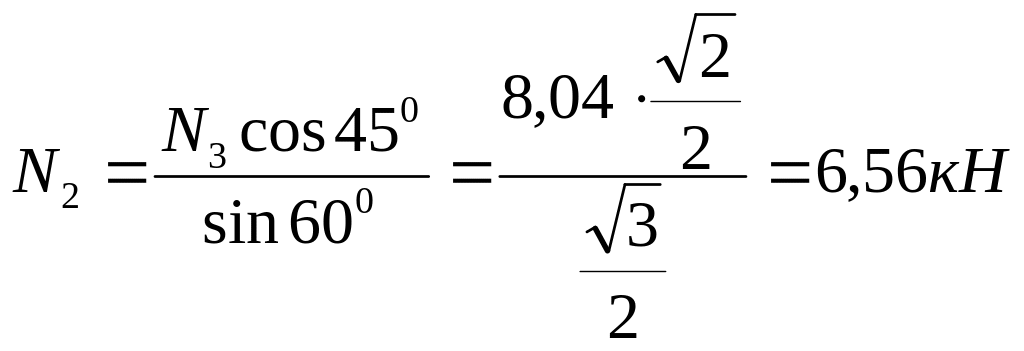
N₂ = 6,56 кН

Определяем площади поперечных сечений стержней

А₁ = в² = 10·10 = 100 мм²

Нормальные напряжения в поперечных сечениях стержней определяем по формуле

Проверка прочности.

Определяем допускаемое напряжение

стержень 1 на 31,25% недогружен,

стержень 2 на 45% перегружен,

стержень 3 на 77,5% перегружен.

Следовательно, надо увеличить диаметр первого стержня и уменьшить диаметры 2 и 3 стержней.

Задача 3.

Определение размеров поперечного сечения стержней.

Емкость для хранения воды, представляет собой конструкцию АВСД, деформацией которой пренебрегаем, прикреплена к фундаменту при помощи стержней 1, 2, 3. Вес конструкции и боковое давление на нее указаны на (рис. 4).

Определить из условия прочности требуемые размеры поперечных сечений стальных стержней, составленных из прокатных профилей, если для стержней, работающих на растяжение, допускаемое напряжение [σ_р] = 160 МПа; для стержней работающих на сжатие, допускаемое напряжение на сжатие [σ_с] = 100 МПа.

Решение.

При расчете стержневых конструкций надо иметь ввиду, что если стержни закреплены по концам шарнирно, то реакции стержней действуют вдоль оси стержня, т.е. имеет место одноосное нагружение.

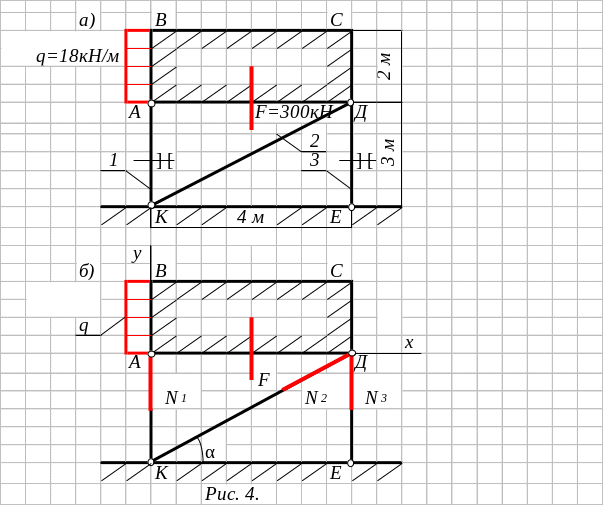
Применяем метод сечений и рассматриваем равновесие конструкции АВСД под действием заданных нагрузок F и q и реакций стержней N₁, N₂, N₃, которые направляем от узлов. В случае, если в результате определения их величин, они окажутся отрицательными, это будет свидетельствовать о том, что их направления первоначально были выбраны неправильно и соответствующий стержень сжат. Полагая все три стержня растянутыми, направляем усилия N₁, N₂, N₃ так, как показано на (рис. 4,б).

Для равновесия конструкции АВСД в плоскости составляют три уравнения равновесия:

- сумма проекций всех сил и сил реакций связей на одну из координатных осей равна нулю:

ΣF_iх = 0;

- сумма проекций всех сил и сил реакций связей на другую ось плоскости действия сил равна нулю:

ΣF_iy = 0;

- сумма моментов всех внешних сил и сил реакций связей относительно любой точки этой плоскости равна нулю:

Σ М_Д (F_i) = 0, где Д произвольна.

Направим координатные оси, как показано на рис. 4, б. Тогда

1. ΣF_iх = q·2 – N₂ cosα = 0

2. ΣF_iy = -N₁ – F – N₂ sinα – N₃ = 0

3. Σ М_Д (F_i) = q·2·1 + N₁·4 + F·2 = 0

Отсюда находим из (3) уравнения

N₁ = -141 кН, т.е. стержень 1 – сжат

из уравнения (1)

где : т.к.

N₂ = 45 кН, т.е. стержень 2 – растянут.

Подставляя N₁ и N₂ в уравнение (2), определим N₃;

+141 – 300 - 45·0,6 - N₃ = 0

N₃ = +141 – 300 – 27,0 = - 186 кН

N₃ = - 186 кН т.е. стержень 3 – сжат.

Определяем площади поперечных сечений стержней. Из условия прочности стержня 1.

Определяем необходимую площадь его поперечного сечения

Так как стержень 1 состоит из двух швеллеров, то площадь поперечного сечения одного швеллера равна

из таблиц Сортимента по ГОСТ 8240-89 ближайший номер швеллера № 6,5, у которого А = 7,51 см².

Выбираем для стержня 1 два швеллера № 6,5 А₁ = 7,51 см².

Из условия прочности стержня 2

Определяем необходимую площадь его поперечного сечения

Так как стержень 2 состоит из двух равнополочных уголков, то

По ГОСТ 8509-86 ближайший уголок № 2 20х20х4 А = 1,46 см².

Выбираем для стержня 2 два равнополочных уголка №2 20х20х4 А=1,46 см².

Из условия прочности стержня 3

Определяем необходимую площадь его поперечного сечения

так как стержень 3 состоит из двух швеллеров, то

по ГОСТ 8240-89 ближайший швеллер № 8 А = 8,98 см²

Выбираем для стержня 3 два швеллера № 8 А = 8,98 см²

Задача 4.

Определение допускаемой нагрузки.

Стержень ВС кронштейна (рис. 5,а) составлен из двух стальных равнополочных уголков 50х50х5, а стержень АВ – из двух стальных швеллеров №8. Определить допускаемые значения силы F, действующей на стальной кронштейн в точке В, если допускаемые напряжения для материала на растяжение [σ_р] = 160 МН/м², [σ_с] = 100 МН/м².

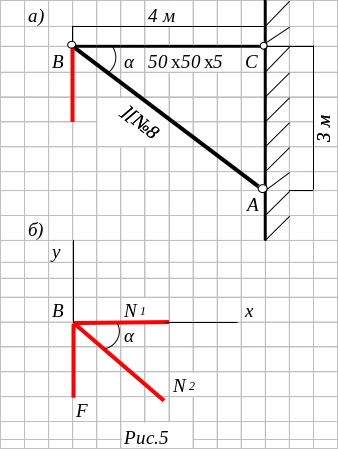
Решение.

Вырежем мысленно узел В (рис.5,б).Обозначим продольную силу в стержне ВС через N₁, а в стержне АВ – N₂ и рассмотрим условие равновесия узла В.

Для данной системы сходящихся сил можно составить два уравнения равновесия:

ΣF_ix = N₁ + N₂·cosα= 0

ΣF_iy = -F - N₂·sinα= 0

Из 2^го уравнения получаем

Следовательно, стержень АВ сжат силой N₂.

Из 1^го уравнения т.е. элемент ВС растянут силой N₁.

Из треугольника АВС определим значение sinα и ctgα. По теореме Пифагора

АВ² = АС² + ВС² отсюда, ;

Тогда ; .

Определяем значения N₁ и N₂, выраженные через силу F.

;

;

Из условия прочности максимальные продольные усилия,

которые можно допустить в поперечных сечения стержней равны:

[N₁] = [σ_р] · A₁ = 160 · 480 · 2 = 921600 Н, где A₁ = 4,8·2 = 9,6 см² для двух уголков 50х50х5.

[N₂] = [σ_с] · A₂ = 100 · 898 = 89800 Н, где A₂ = 8,98 см² для швеллера № 8.

Следовательно, исходя из расчета прочности кронштейна по слабому звену, допустимая нагрузка из соотношения N₂ = -1,67 F равна

Ответ: [F] =53,8 кН.

Задача 5.

Определить допускаемую толщину t растягиваемого листа, ослабленного отверстиями d = 2 см, а ширина листа в = 24 см, предел текучести σ_т = 240МПа, коэффициент запаса прочности n_т = 1,5. Внешняя растягивающая сила F = 180 кН.

Решение.

Внутренняя продольная сила в любом поперечном сечении бруса

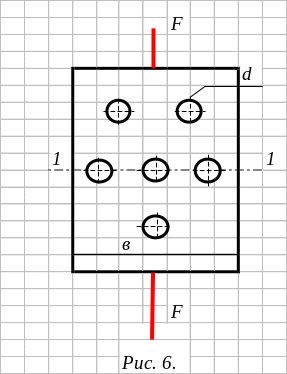
N = F = 180 кН (рис. 6). По известному предельному напряжению σ_пред = σ_т и коэффициенту запаса прочности определяем [σ], которое равно

Таким образом, известными величинами являются внутренняя сила N и допускаемое напряжение [σ]. Из расчетного уравнения при растяжении

видим, что неизвестной величиной является площадь поперечного

сечения А, которая будет равна

Ослабленным сечением стального листа является сечение 1-1 (рис. 6), в котором расположены три отверстия. Площадь поперечного сечения 1-1 равна А = в·t - 3·td = t·(в - 3d), откуда

т.е.

Задача 6.

Определить, какой должен быть площадь квадратного поперечного сечения деревянной колонны из сосны с модулем упругости Е = 1·10⁴ МПа (рис. 7), чтобы опускание верхнего конца колонны не превышало [∆ℓ] = 0,3 см.

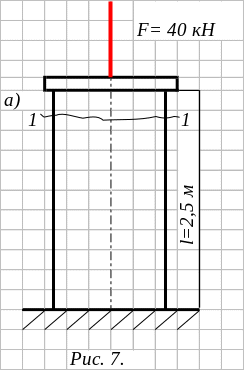
Решение.

Оценка жесткости бруса проводится на основе проверки условия жесткости при растяжении или сжатии ∆ℓ ≤ [∆ℓ]. (1)

Величина допускаемой абсолютной деформации [∆ℓ] назначается отдельно для каждой конструкции. Условие жесткости предполагает три вида расчетов:

1. проверка жесткости данного элемента конструкции, т.е. проверка выполнения условия (1).

2. расчет проектируемого стержня, т.е. подбор его поперечных размеров. Из условия жесткости

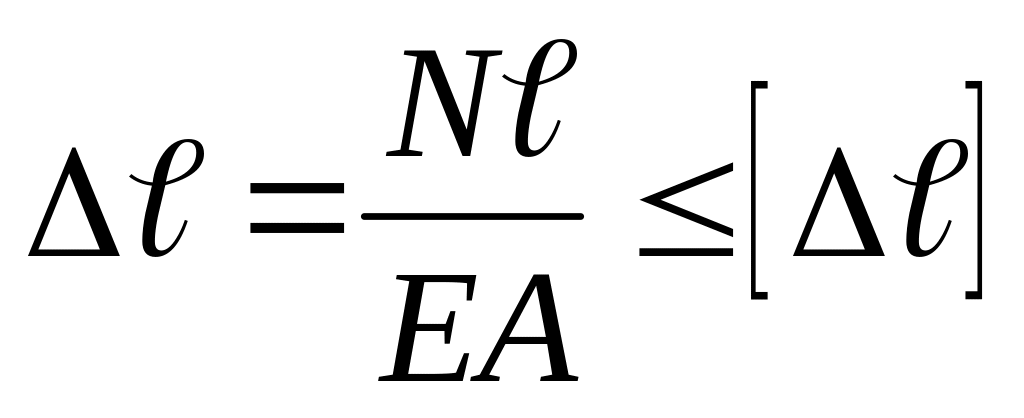
где N – внутренняя сила в поперечном сечении бруса или стержня, ℓ - длина, Е – модуль упругости при растяжении или сжатии, А – площадь поперечного сечения, которую определяют

3) установка работоспособности данного стержня, т.е. определение допускаемой нагрузки

В данном примере требуется выполнить проектировочный расчет стержня. Применив метод сечений, определяем внутреннюю силу в поперечном сечение бруса. Проведем сечение 1-1 и рассмотрим верхнюю часть бруса, направив продольную силу N в сторону отброшенной части бруса (рис. 7,б).

Составив уравнение равновесия ΣF_iy = F + N = 0; получаем N=-F =- 40 кН (сжатие).

Для определения площади колонны запишем условия жесткости:

, отсюда

Так как сечение колонны квадратное, то А = а², где а – сторона квадрата. Следовательно ; принимаем .

Проверим, будет ли выполняться условие прочности при данной площади поперечного сечения. Допускаемое напряжение на сжатие для сосны [σ] = 12 МПа, тогда напряжение, возникающее при действии силы N,

Условие прочности выполняется.