
- •4.Порівняння чисел в десятковій системі числення.
- •10.Дії над числами в різних позиційних системах числення ,відміних від десяткової.
- •13.Теорема про подільність суми двох цілих невід’ємних чисел.
- •28. Поняття дробу і додатного раціонального числа. Множина додатних раціональних чисел, її властивості.
- •29.Поняття дробу. Основна властивість дробу. Рівність дробів. Порівняння дробів.
- •30. Додавання дробів. Закони додавання.
- •31.Віднімання дробів
- •32. Множення дробів. Закони множення.
- •33. Ділення дробів
- •34. Запис додатних раціональних чисел у вигляді скінченних десяткових дробів.
- •2)Домножити чисельник і знаменник на необхідні степені чисел 2 і 5 так, щоб знаменник дорівнював числу 10k
- •35. Запис додатних раціональних чисел у вигляді відсотків. Розв'язування задач з відсотками.
- •1 Відсоток - це одна сота частина числа.
- •37. Необхідність розширення множини додатних раціональних чисел. Поняття додатного ірраціонального числа.
- •I крок.
- •II крок.
- •38. Додатні ірраціональні числа. Множина додатних дійсних чисел, її властивості.
- •40. Множення і ділення додатних дійсних чисел.
- •41. Від’ємні дійсні числа. Множина дійсних чисел, її властивості.
- •42. Модуль дійсного числа. Виконання арифметичних дій над дійсними числами.
- •Правила виконання арифметичних дій над дійсними числами:
- •43. Величини та їх вимірювання.
- •1. Величина як властивість предметів або явищ реального світу. Вимірювання величин. Властивості скалярних величин.
- •44. Поняття вимірювання величини. Міжнародна система одиниць вимірювання величин.
- •46. Одиниці вимірювання довжини відрізка. Дії над числовими значеннями довжин відрізків.
- •47. Довжина відрізка та її вимірювання.Властивості числових значень довжини.
- •48. Площа фігури та її вимірювання. Стандартні одиниці вимірювання площі.
- •49. Площа фігури.Стандартні одиниці вимірювання площі.
- •50.Площа фігури. Обчислення площ многокутників і площ поверхонь геометричних тіл.
- •51. Площа фігури. Вимірюванняплощіфігури за допомогою палетки.
- •52. Маса тіла, її вимірювання. Стандартні одиниці вимірювання маси тіла.
- •53. Одиницівимірюваннямаситіла.Дії над числовимизначеннямимаситіла.
- •54. Маса тіла. Властивості числових значень маси тіла.
- •55. Час, його вимірювання. Стандартні одиниці вимірювання часу.
- •56. Час, його властивості.
- •57. Об’єм тіла, його вимірювання. Стандартні одиниці вимірювання об’єму.
- •58. Об’єм тіла, його вимірювання. Стандартні одиниці вимірювання об’єму.
40. Множення і ділення додатних дійсних чисел.
Означення.
Добутком додатних дійсних чисел
називають число, яке задовольняє умову:
 ,
,
де - наближені значення чисел з недостачею,
 -
наближені
значення чисел
з
надлишком.
-
наближені
значення чисел
з
надлишком.
Дія, за допомогою якої знаходять добуток, називається множення. Числа при множенні називаються I множник,II множник, добуток.
Приклад 1. Знайдемо добуток чисел
1,41

1,41
2,4393
З
точністю до 0,01

Властивості:
 -
переставний закон
-
переставний закон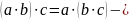 сполучний
закон
сполучний
закон -
розподільний
закон множення відносно додавання(віднімання)
-
розподільний
закон множення відносно додавання(віднімання)Добуток двох доданих дійсних чисел завжди існує і єдиний.
Означення.
Часткою двох додатних дійсних чисел
називається
таке додатне дійсне число
 що
що
 .
.
Частка будь-яких додатних дійсних чисел завжди існує і єдина.
Дія, за допомогою якої знаходять частку, називається ділення. Ділення – обернена дія до множення.
 .
.
Числа при діленні називається ділене, дільник, частка.
Приклад 2. Знайдемо частку чисел і .
1,73
1,41
1,73:1,41

1,220
З
точністю до 0,1:

41. Від’ємні дійсні числа. Множина дійсних чисел, її властивості.
Розглянемо
координатну пряму
 .
.
![]()
Праворуч
від точки
 розміщують
точки, які зображають додатні дійсні
числа.
розміщують
точки, які зображають додатні дійсні
числа.
 - одиничний відрізок, точці
- одиничний відрізок, точці
 відповідає координата 1, тобто
відповідає координата 1, тобто
 .
Відкладемо вліво одиничний відрізок
.
Відкладемо вліво одиничний відрізок
 ,
одержимо точку
,
одержимо точку
 ,
симетричну точці
відносно точки
.
Координату точки
позначимо – 1, тобто
,
симетричну точці
відносно точки
.
Координату точки
позначимо – 1, тобто
 .
Аналогічно
.
Аналогічно
 і
т.д.
і
т.д.
Числа 1 і (-1); 2 і (-2) називаються протилежними.
Числа, розміщені на координатній прямій в заданому напрямку (вправо називаються додатними, а числа, розміщені на координатній прямій в напрямку, протилежному до даного (вліво) називаються від’ємними. Число є ні додатним, ні від’ємним.
Означення.
Від’ємним дійсним числом називають
число виду
 .
.
Всі
від’ємні дійсні числа складають множину
від’ємних дійсних чисел

- це множина додатних дійсних чисел.
 -
це множина від’ємних дійсних чисел.
-
це множина від’ємних дійсних чисел.
 -
множина дійсних чисел.
-
множина дійсних чисел.
 .
.
Означення. Об’єднання множини від’ємних дійсних чисел з множиною додатних дійсних чисел і нулем називаються множиною дійсних чисел і позначаються .
Отже, множина дійсних чисел розбивається на три класи: клас додатних від’ємних чисел, клас додатних дійсних чисел і число 0.
На координатній прямій кожному дійсному числу ставиться у відповідність єдина точка і навпаки.
Властивості множини :
1)нескінченність, немає найбільшого і найменшого дійсного числа;
2)упорядкованість,
бо встановлюється відношення лінійного
порядку: це відношення
,
яке має властивості: антисиметричність
(якщо
,
то
 ;
транзитивність ( якщо
,
і
;
транзитивність ( якщо
,
і

3)щільність;
бо для будь-якої пари дійсних чисел
 існує таке дійсне число
,
що
існує таке дійсне число
,
що

4)незчисленність, бо її числа не можна пронумерувати натуральними числами ( не рівнопотужна ).
42. Модуль дійсного числа. Виконання арифметичних дій над дійсними числами.
Означення. Модулем дійсного числа називається відстань від точки відліку до точки, яка відповідає цьому числу.
Модуль
(абсолютна величина) числа
позначається
 - це –
- це –
1)саме це число, якщо воно додатне;
2)протилежне йому число, якщо воно від’ємне;
3)нуль, якщо воно рівне нулю.
Отже,
=

Модуль будь-якого дійсного числа є завжди невід’ємним числом.
Два протилежних числа мають той самий модуль, що дорівнює додатному з цих чисел, наприклад :
 .
.
Модуль нуля є нуль.
З двох відємних чисел те число більше, модуль якого менший.

![]()
-4<-2
але 2<4,
тобто

