30. Додавання дробів. Закони додавання.

Означення. Якщо додатні раціональні числа 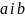представлені дробами і 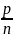, то сумою чисел називається число, зображене дробом .

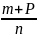Отже, правило: + = .

Наприклад : + = = .

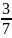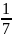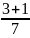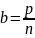, -доданки, а операція знаходження суми називається додаванням.

Якщо додатні раціональні числа представлені дробами з різними знаменниками, то ці дроби зводять до спільного знаменника і додають за правилами додавання дробів з однаковими знаменниками.

Закони додавання:

1)переставний: 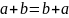, для , , - додатні раціональні числа.

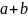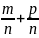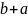Доведення: якщо , , то = = = = , бо натуральні числа.

2)сполучний закон , для , , .

додатні раціональні числа.

Теорема.

Сума додатних раціональних чисел завжди існує і єдина.

31.Віднімання дробів

Означення.

Різницею додатних раціональних чисел називають таке додатне раціональне числоc , що a=b +c.

a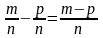 –зменшуване, b -від’ємник, операція знаходження різниці – віднімання.

Якщо, , то .

За означенням різниці:

b+c= .

Отже,a = b+c.

Віднімання дробів.

Правило.

Наприклад:

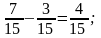
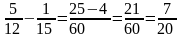
Теорема.

Нехай a, b є Q₊, різниця a - b існує тоді і тільки тоді, коли a>b. Якщо різниця існує, то вона єдина.

32. Множення дробів. Закони множення.

Означення. Якщо додатні раціональні числа представлені дробами i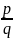 , то їх добуток є число , записане дробом 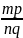. 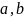- множники, операція знаходження добутку – множення.

Правило: .

Наприклад: .

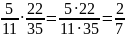Закони множення: = , , ;

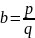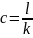1)переставний: .

2) сполучний: .

3)розподільний закон множення відносно додавання(віднімання)

.

Доведення переставного закону:

. Для натуральних чисел

Отже, .

Теорема. Для будь-яких додатних раціональних чисел існує добуток і при тому єдиний.

33. Ділення дробів

Означення.Часткою двох додатних раціональних чиселaib називається таке число c, що a = bc.

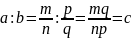Якщо , , то , бо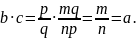

Отже, b · c = a.

Правило: .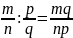

Наприклад :

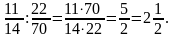
a :b = c, a-ділене,b - дільник, c- частка.

Операція знаходження частки називається діленням.

Теорема.

Для будь-яких додатних раціональних чиселaibіснує часткаa : b і при тому єдина.

34. Запис додатних раціональних чисел у вигляді скінченних десяткових дробів.

- звичайний дріб, 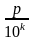- десятковий дріб.

Означення:Дріб виду записаний у позиційній десятковій системі числення, називають десятковим.

Наприклад:

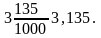
Порівняння десяткових дробів і виконання дій над ними зводиться до порівняння і дій над натуральними числами.

Наприклад: 0,347 < 0,375 ( 4<7). ,

Теорема.Для того, щоб звичайний нескоротний дріб перетворювався у десятковий, необхідно і достатньо, щоб канонічний розклад його знаменника містив лише прості множники 2 і 5.

Наприклад:дріб 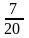— можна записати у вигляді десяткового, бо 20 = 2² · 5, а дріб не можна записати у вигляді скінченного десяткового дробу, бо 15 = 5 · 3.

Способи перетворення звичайного дробу в десятковий.

1) чисельник звичайного дробу поділити на знаменник: бо

130 20

120 0,65

100

100

0