28. Поняття дробу і додатного раціонального числа. Множина додатних раціональних чисел, її властивості.

Приклад1.

Візьмемо відрізок . Щоб знайти його довжину, виберемо одиницю довжини . При вимірюванні виявилось, що довжина відрізка більша, ніж , але менше ніж 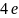, тобто . Томі її не можна виразити натуральним числом(при одиниці довжини ).

Розіб’ємо відрізок на 4 рівні частини, кожна з яких рівна , тоді =13 =13 = . Символ - називається дробом.

У загальному вигляді поняття дробу визначають так:

Нехай дано відрізок і одиничний відрізок , причому відрізок є сумою відрізків, рівних . Якщо відрізок складається з відрізків, рівних , то його довжина може бути представлена у вигляді . Символ називається дробом, де - натуральні числа. Читають цей символ «ем енних»! - чисельник, - знаменник. – показує, на скільки рівних частин розділено одиничний відрізок , а - показує, скільки взято таких частин. При вимірюванні відрізка у прикладі 1 використовували відрізок - четверту частину відрізка , одержали .

Для вимірювання відрізка можна взяти восьму частину відрізка , тоді , але можна взяти і шістнадцяту частину відрізка , тоді і так далі.

Дроби , , - виражають довжину відрізка .

Означення. Дроби, що виражають довжину одного і того ж відрізка при одиниці довжини називаються рівними дробами.

Отже, = .

Додатне раціональне число – це множина рівних дробів, а кожний дріб, що належить цій множині, є записом (представленням) цього числа.

Наприклад: множина є деяке раціональне число, а дроби 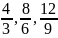і т. д. –це різні записи цього числа.

Серед всіх записів деякого додатного раціонального числа виділяють нескоротний дріб, в якому знаменник і чисельник взаємно-прості числа(їх найбільший спільний дільник – 1).

Для будь-якого додатного раціонального числа існує один і тільки один нескоротний дріб, що є записом цього числа.

Дроби розрізняють:

правильні - (

неправильні - (

мішані - (ціла частина і дробова)

Необхідність виразити точно довжину відрізка єдиним числом привела до появи додатних раціональних чисел.

- множина додатних раціональних чисел.

- це об’єднання множини натуральних чисел ( ) і множини додатних дробових чисел.

. Кожне натуральне число можна записати у вигляді дробу:

1= , 7= .

Властивості множини :

1)нескінченість: немає найменшого і найбільшого додатного раціонального числа;

2)щільність (між будь-якими двома різними додатними раціональними числами є нескінчена кількість чисел цієї множини).

3)упорядкованість, бо на множині можна ввести відношення «менше», яке транзитивне (якщо то , і антисиметричне (якщо , то , тобто є відношення порядку.

29.Поняття дробу. Основна властивість дробу. Рівність дробів. Порівняння дробів.

-Символ називається дробом, де і натуральні числа, -чисельник, - знаменник. Наприкалад: , , .

Означення. Дроби, що виражають довжину одного і того ж відрізка при одиниці довжини , називаються рівними дробами.

Запис: . Наприклад = (3 і 4 помножили на 2).

Основна властивість дробу. Якщо чисельник і знаменник дробу помножити, або поділити на одне й те ж натуральне число, то вийде дріб рівний даному.

Теорема. Для того, щоб дроби і були рівними, необхідно і достатньо, щоб

Доведення.

Необхідність.

Якщо , то .

Дано: дроби і ,

Довести: .

За умовою , розділимо обидві частини рівності на число , одержимо правильну рівність: .

Але ( скоротили на ), а (скоротили на ; за основною властивістю дробу).

За доведенням , тоді .

Отже, якщо , то .

Необхідність доведено.

Достатність:

Якщо дроби і , - рівні, то .

Дано: = .

Довести: . .

За умовою = .

Оскільки ( за основою властивістю дробів),а ( за основою властивістю дробів), тоді

Якщо дроби рівні, їх знаменники рівні, тоді і знаменники рівні, тобто .

Отже, якщо = . , то .

Достатність доведено.

Порівняння дробів Якщо і , то , тоді і тільки тоді, коли . Наприклад: , , , бо 11·8=88; 13·7=91, звідси 11·8<13·7.

2) Якщо , , то тоді і тільки тоді, коли (знаменники однакові, то порівнюють чисельники).

Наприклад: , бо 4 7.

3) Якщо , , то тоді і тільки тоді, коли (чисельники однакові, то порівнюють знаменники).

Наприклад: , бо 5 3.