49. Площа фігури.Стандартні одиниці вимірювання площі.

Площа - це одна із скалярних величин, деяка властивість об'єктів реального світу (підлоги, земельної ділянки, Атлантичного океану, Житомирської області).Площею фігури називається додатна величина, визначена для кожної фігури так, що:1) рівні фігури мають рівні площі:2)якщо фігура складається із скінченої кількості фігур, які не мають спільнихточок, то її площа дорівнює сумі їх площ. Площа фігури має такі самі властивості, як і довжина. Різниця лише в тому, що довжину ми розглядаємо на множині відрізків, а площу - на множині фігур. Площу фігури прийнято позначати буквою S.

Площа фігури має такі властивості:

1.Площі можна порівнювати: F₁ = F₂<=>S (F₁) = S (F₂):

F₁>F₂<=> S (F₁) > S (F₂).

2. Якщо F = F₁+F₂, то S (F) = S (F₁) + S (F₂).

3. Якщо F = F₁-F₂, то S (F) = S (F₁) - S (F₂).

4. Якщо фігура F₁має площу S (F₁),то фігура k · F₁має площу

S (F) = k · S ( F₁).

5. S ( F₁) : S ( F₂) = k,де k - деяке дійсне число.

50.Площа фігури. Обчислення площ многокутників і площ поверхонь геометричних тіл.

Площа - це одна із скалярних величин, деяка властивість об'єктів реального світу (підлоги, земельної ділянки, Атлантичного океану, Житомирської області).

Площею фігури називається додатна величина, визначена для кожної фігури так, що:

1) рівні фігури мають рівні площі:2)якщо фігура складається із скінченої кількості фігур, які не мають спільних

точок, то її площа дорівнює сумі їх площ.

Об'єднання простої замкненої лінії та її внутрішньої області називається многокутником. Ланки ламаної називаються сторонами многокутника.Точки, в яких збігаються дві суміжні ланки, називаються вершинами многокутника. Відрізок, що з'єднує дві вершини многокутника, які не належать одній з його сторін, називається діагоналлю.Залежно від кількості сторін многокутник називається трикутником, чотирикутником, п'ятикутником тощо.Для обчислення площ многокутників використовуються такі формули:

прямокутник:

S= · b, де , b - сторони прямокутника;

S = d²·sin , де - діагональ прямокутника, - кут між діагоналями;

квадрат:

S= ², де - сторона квадрата;

S= 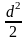, де d - діагональ квадрата;

паралелограм:

S= · h, де - сторона паралелограма, Н - висота, проведена до цієї сторони;

S = d₁ ·d₂ · sin , де d_1,d₂ - діагоналі паралелограма, - кут між діагоналями;

S= · b ·sin ,де , b - сторони паралелограма, - кут паралелограма;

ромб:

S = 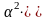sin , де - сторона ромба, - кут ромба;

S= · h, де - сторона ромба, h - висота, проведена до цієї сторони;

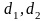S = де - діагоналі ромба;

трапеція:

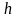S = де - основи трапеції, - її висота;

S= 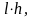де - середня лінія трапеції, h - її висота;

трикутник:

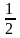
S= , де - сторона трикутника, h - висота, проведена до цієї сторони; .

S= , де 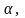- сторони трикутника, - кут між ними;

S= 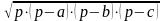, де 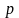- півпериметр трикутника (формула Герона);

правильний (рівносторонній) трикутник:

S =

прямокутний трикутник:

S = де a, b- катети цього трикутника.

площу круга обчислюють за формулами:

S= , де 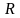- його радіус;

S = 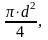де 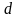- діаметр круга.

Площі поверхонь геометричних тілзнаходять за такими формулами:

пряма призма:

бічна поверхня 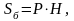де - периметр основи призми, 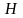- її висота (бічне ребро);

повна поверхня 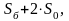де 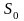- площа основи призми;

правильна піраміда:

бічна поверхня 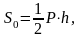де - периметр основи піраміди, - апофема (висота бічної грані);

повна поверхня де - площа основи піраміди;

циліндр:

бічна поверхня 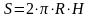, де - радіус основи циліндра, - висота (твірна);

повна поверхня

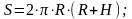
конус:

бічна поверхня де - радіус основи конуса, - його твірна;

повна поверхня

сфера: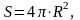 де - радіус сфери (кулі).