39. Понятие статистической гипотезы. Нулевая и конкурирующая, простая и сложная гипотезы. Ошибки первого и второго рода. Уровень значимости статистического критерия. Мощность критерия.

Статистич. гипотеза – некоторое предположение, формулируемое на основе выборки, о законе распределения СВ или о параметрах этого закона. Проверяемую гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, называют нулевой (основной) гипотезой и обозначают . Гипотезу , являющуюся логическим отрицанием , называют альтернативной (конкурирующей) гипотезой, т.е. если гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза . часто спец.-но подбирается так, чтобы отвергнуть её и принять альтернативную. Гипотеза называется простой, если она содержит только 1 предположение. Гипотеза называется сложной, если она состоит от конечного или бесконечного множества простых гипотез. Принятие или отклонение выдвинутой гипотезы соответствует истине с некоторой вероятностью. Ошибка первого рода возникает с вероятностью α тогда, когда отвергается верная гипотеза и принимается конкурирующая гипотеза : . Вероятность α называется уровнем значимости. Ошибка второго рода возникает с вероятностью в том случае, когда принимается неверная гипотеза в то время как справедлива конкурирующая гипотеза . Мощность критерия( ) или — вероятность отклонить гипотезу , если на самом деле верна альтернативная гипотеза . Мощность критерия является числовой функцией от альтернативной гипотезы .

40. Статический критерий проверки нулевой гипотезы. Области принятия и отклонения гипотезы. Построение критической области. Основные этапы проверки гипотезы.

Статистический критерий представляет из себя определенное правило, устанавливающее условия, при которых проверяемую нулевую гипотезу нужно либо отклонить, либо не отклонять. Критерий проверки статистической гипотезы определяет, противоречит ли выдвинутая гипотеза фактическим данным или не противоречит. Критическая область( ) представляет из себя область, попадание в которую значения статистического критерия приводит к отклонению . Вероятность попадания значения критерия в такую область равняется принятому уровню значимости. Если вычисляемое значение критерия попадет в критическую область, то отклоняется, так как она противоречит фактическим данным. В зависимости от формулировки альтернативной гипотезы критическая область может быть левосторонняя или правосторонняя, двухсторонняя или односторонняя. Область допустимых значений (принятия гипотезы - w) дополняет критическую область. Если значение критерия попадает в данную область, то это может говорить о том, что выдвинутая гипотеза не противоречит фактическим данным, т. е. Нo не отклоняется. Построение критической области. Из области значений выделяется подмножество таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство . Это множество и называется критической областью. Вероятность того, что критерий примет значение из критической области должна быть минимальной и равной заданному числу α, если верна , и максимальной в противном случае, т.е. критическая область должна быть такой, чтобы при заданном уровне значимости α, мощность критерия была бы максимальной.

Основной принцип проверки стат.-ой гипотезы: если значение критерия попадает в область w, то гипотеза принимается, а если в область - гипотеза отклоняется.

Общая схема проверки гипотез (основные этапы):

1. Формулировка проверяемой (нулевой - ) и альтернативной( ) гипотез.

2. Выбор соответствующего уровня значимости α.

3. Определение объёма выборки n.

4. Выбор критерия для проверки .

5. Определение критической области и области принятия гипотезы.

6. Вычисление наблюдаемого значения критерия набл.

7. Принятие статистического решения.

41. Проверка гипотезы о равенстве средних двух генеральных совокупностей при известных и неизвестных дисперсиях. Распределение случайной величины называют распределением Стьюдента с K степенями свободы и обозначают .

При известной дисперсии: Случайная величина приближенно подчиняется стандартному нормальному распределению 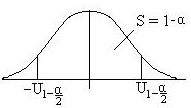. Из рисунка видно, что вероятность Получаем критерий при уровне значимости α:

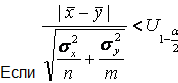
, то гипотеза принимается, в противном случае гипотеза отвергается в пользу .

При неизвестной дисперсии: в предположении, что генеральные дисперсии одинаковы, требуется проверить гипотезу против = {ax ≠ ay}. Критерий основан на следующем факте: Случайная величина приближённо подчиняется распределению Стьюдента с (n+m–2)-cтепенями свободы при растущих n и m. Аналогично предыдущему случаю получаем критерий при уровне значимости a: Если , то гипотеза принимается, в противном случае гипотеза отвергается в пользу . Здесь – выборочные средние, α – уровень значимости, – квантиль распределения Стьюдента, – выборочные дисперсии случайных величин ξ и η. Замечание (о распределении Стьюдента): при увеличении n распределение Стьюдента асимптотически приближается к стандартному нормальному распределению. Поэтому для больших n в таблицах надо смотреть квантиль нормального стандартного распределения.