35. Статистическое оценивание параметров распределения по выборке. Понятие оценки параметра распределения. Свойства оценки: несмещённость, состоятельность, эффективность.

Если из теоретических соображений удалось установить, какое именно распределение имеет признак, то возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак генеральной совокупности распределен нормально, то необходимо оценить /приближенно найти/ математическое ожидание a и среднее квадратичное отклонение . Обычно в распоряжении исследователя имеются лишь данные выборки. Через эти данные и выражают оцениваемый параметр. (Оценка бывает точечной и интервальной: точечной – если определяется одним числом; интервальной – если по данным выборки строится числовой интервал, внутри которого на основании заранее выбранной вероятности находится оцениваемый параметр.)

Оценкой параметра называется любая функция от значений выборки , т.е. статистика. Оценка должна быть близка к оцениваемому параметру. Близость характеризуется несмещенностью оценки, её состоятельностью и эффективностью. Оценка является несмещённой, если . Если для любого то оценка называется состоятельной. Оценкой качества несмещенной оценки является ее дисперсия. Несмещенная оценка называется эффективной, если ее дисперсия является наименьшей среди дисперсий всех возможных оценок параметра , вычисленных по одному и тому же объему выборки n. Оценки называются точечными, так как они оценивают одно численное значение параметра (точку). Точечная оценка параметра дает лишь некоторое приближенное значение . Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.

36. Точечные оценки мат. Ожидания и дисперсии. Частость как точечная оценка вероятности события. Свойства этих точечных оценок.

Точечная оценка математического ожидания. Задана случайная величина Х: х1, х2, …, хn, так как М(Х) не найти, то для математического ожидания случайной величины Х естественно предложить среднее арифметическое её наблюденных значений. 1)По методу произведений , так как Это и означает, что оценка несмещенная.

2. Если исследуемая случайная величина Х имеет конечную дисперсию, то эта оценка будет состоятельной, так как 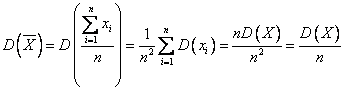Если исследуемая величина имеет нормальный закон распределения, то можно показать, что предложенная оценка эффективна, т. е. оценки для математического ожидания с меньшей дисперсией не существует для нормально распределенных величин.

Точечная оценка для дисперсии. Так как дисперсия определяется через математическое ожидание, а для математического ожидания оценка уже выбрана, то для дисперсии естественно предложить оценку: или ; , что соответствует записи дисперсии в виде . Оказывается, что предложенная оценка дисперсии состоятельна (легко доказать) и не является несмещенной. Чтобы в этом убедиться, возведём в квадрат последнее слагаемое: Процентрируем величину Х, т. е. перенесем начало координат в точку М(Х): . Дисперсия зависит лишь от разности значений Х и математического ожидания, поэтому от переноса начала координат оценка не изменится и равенство можно продолжить: Вычислим теперь математическое ожидание полученной величины т. е. , так как . Значит, предложенная оценка занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку и полученную оценку обозначим через S^2 или Оценка S^2 является состоятельной, так как сходится по вероятности к М(Х^2), а – к М(Х). Замечание. При малых n дробь довольно значительно отличается от единицы, а с увеличением n стремится к единице. При n > 50 практически нет разницы между оценками и S^2. Оценки и S^2 являются состоятельными оценками дисперсии.

Частость как точечная оценка вероятности события. Обозначим через р неизвестную вероятность появления случайного события А в единичном испытании. Приближенное значение вероятности р определяется в виде , где - частость появления события А в n испытаниях; m - число появления события А в n испытаниях. Серия независимых испытаний, в каждом из которых событие А происходит с вероятностью q=1-p, является последовательностью испытаний Бернулли. Теорема. Пусть m - число наступлений события А в n независимых испытаниях, р - вероятность наступления события А в каждом из испытаний. Тогда - состоятельная , несмещенная и эффективная оценка вероятности р.

Свойства точечных оценок. 1)Оценка называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности: , где обозначает мат. ожидание в предположении, что — истинное значение параметра (распределения выборки ).

2) Оценка называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.

3) Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: , по вероятности при .

4) Оценка называется сильно состоятельной, если , почти наверное при . Надо отметить, что проверить на опыте сходимость «почти наверное» не представляется возможным, поэтому с точки зрения прикладной статистики имеет смысл говорить только о сходимости по вероятности.