Система пар сил.

Системой пар сил является совокупность пар сил, приложенных к одному телу.

Сложение пар сил. Система пар сил эквивалентна одной паре, момент которой равен сумме моментов пар, образующих систему:

(8)

где M₁ = M(F₁,F₁'), M₂ = M(F₂,F₂'), ..., M_n = M(F_n,F_n').

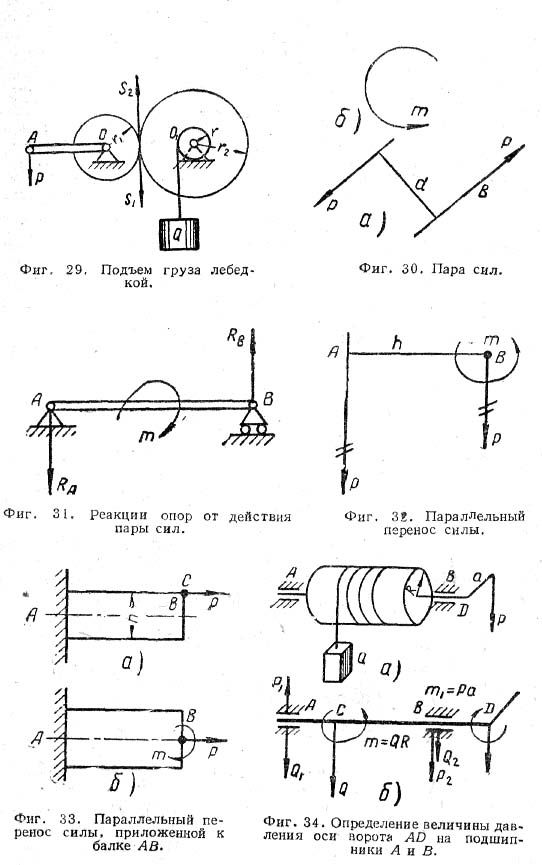
Моментом пары сил называется взятое со знаком (+) или (-) произведение величины одной из сил на ее плечо: m = ±Pd. Момент пары считается положительным, если пара стремится вращать тело против вращения часовой стрелки. Пару сил принято изображать изогнутой стрелкой (фиг.30, б). Буква у конца стрелки обозначает момент пары.

Условие равновесия пар: для равновесия нескольких пар необхо­димо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

Момент пары сил не имеет точки приложения (Вторая теорема Вариньона): к каким бы частям твёрдого тела ни прикладывались силы, при данных величине и направлении момента сил вращаться оно будет одинаково.

Действие силы, приложенной к твёрдому телу на некотором расстоянии d от центра масс (в точке, в которую из центра масс можно провести вектор  ), эквивалентно дествию такой же силы, приложенной непосредственно к центру масс, комбинированной с некоторой парой сил, такой, что  , то есть с моментом, равным моменту силы относительно центра масс (в частности, если  , можем задаться  , в таком случае одна из сил будет приложена в той же точке, что и исходная, и составит  ).

11. Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Доказательство: Пусть на твердое тело действует пара сил .

Перенесем силу  в точку , а силу  в точку . Проведем через точки две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки  отрезком прямой и разложим силы в точке  и  в точке  по правилу параллелограмма.

Так как , то

и

Поэтому эквивалентна системе , а эта система эквивалентна системе , так как эквивалентна нулю.

Таким образом мы заданную пару сил  заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.

Момент исходной пары сил  численно равен площади параллелограмма , а момент пары сил  численно равен площади параллелограмма . Но площади этих параллелограммов равны, так как площадь треугольника равна площади треугольника .

Что и требовалось доказать.

Выводы:

1.      Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

2.      У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

14.