30. Вращение точки вокруг неподвижной оси.

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, все время остаются неподвижными.

Прямая, проходящая через 2 указанные неподвижные точки наз.ОСЬЮ ВРАЩЕНИЯ.

Точки тела,не лежащие на оси описывают окружности, плоскости проходят перпердикулярнооси,а центр вращения лежат на оси.

Рассмотрим вращение твердого тела (рис. 2.11) вокруг оси, проходящей через две неподвижные точкиО и О₁ Проведем через ось неподвижную полуплоскость и движущуюся вместе с телом полуплоскость . Вращение тела будет определяться величиной ф двугранного угла между по-луплоскостями и . Угол называется углом поворота. Условимся считать за положительное направление вращения тот случай, когда, смотря с заданного направления оси вращения, увеличение угла поворота наблюдается в сторону, противоположную движению часовой стрелки.

П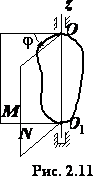 ри вращении угол поворота изменяется в зависимости от времени. Равенство: -уравнение вращения тела вокруг неподвижной оси.В частном случае,когда φ «+»ее в начальный момент,когда совпалает неподвижн. И подвижн.полуплоскости,угловая координата соответствует углу поворота тела. Хар-кой быстроты служит угловая скорость.Исходя из определения производной как скорости изменения ф-ий и зависимости от времени tслужит ее производная по времени ɷ= =φЕсли производная φ ,то движение будет возростать и наоборот.Хар-кой изменения скорости явл-ся ускорение,т.е.угловым ускорением наз-ся производная от угловой корости по времени.

31. Равномерное вращение тела.Равнопеременное вращательное движение тела.Равномерным движением наз-ся движение тела, при котором угол поворота тела уменьшается пропорционально времени. φ=ɷt угловая скорость при этом должна быть постоянной.ɷ= 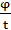=const.Вращательное движение тела в зависимости от времени t характеризуют угловые величины: φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек2). Закон вращательного движения тела выражается уравнением φ = f (t). Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени ω = dφ/dt = f' (t). Вращательное движение тела называется равнопеременным, если во все время движения угловое ускорение тела постоянно (ε = const).

Если угловое ускорение положительно, то вращение называется равноускоренным; если оно отрицательно — вращение равнозамедленное.При равнопеременном вращательном движении формулы имеют аналогичное изображение как для поступательного, так и для вращательного движения.

32. Скорости и ускорения точек вращающегося тела.

О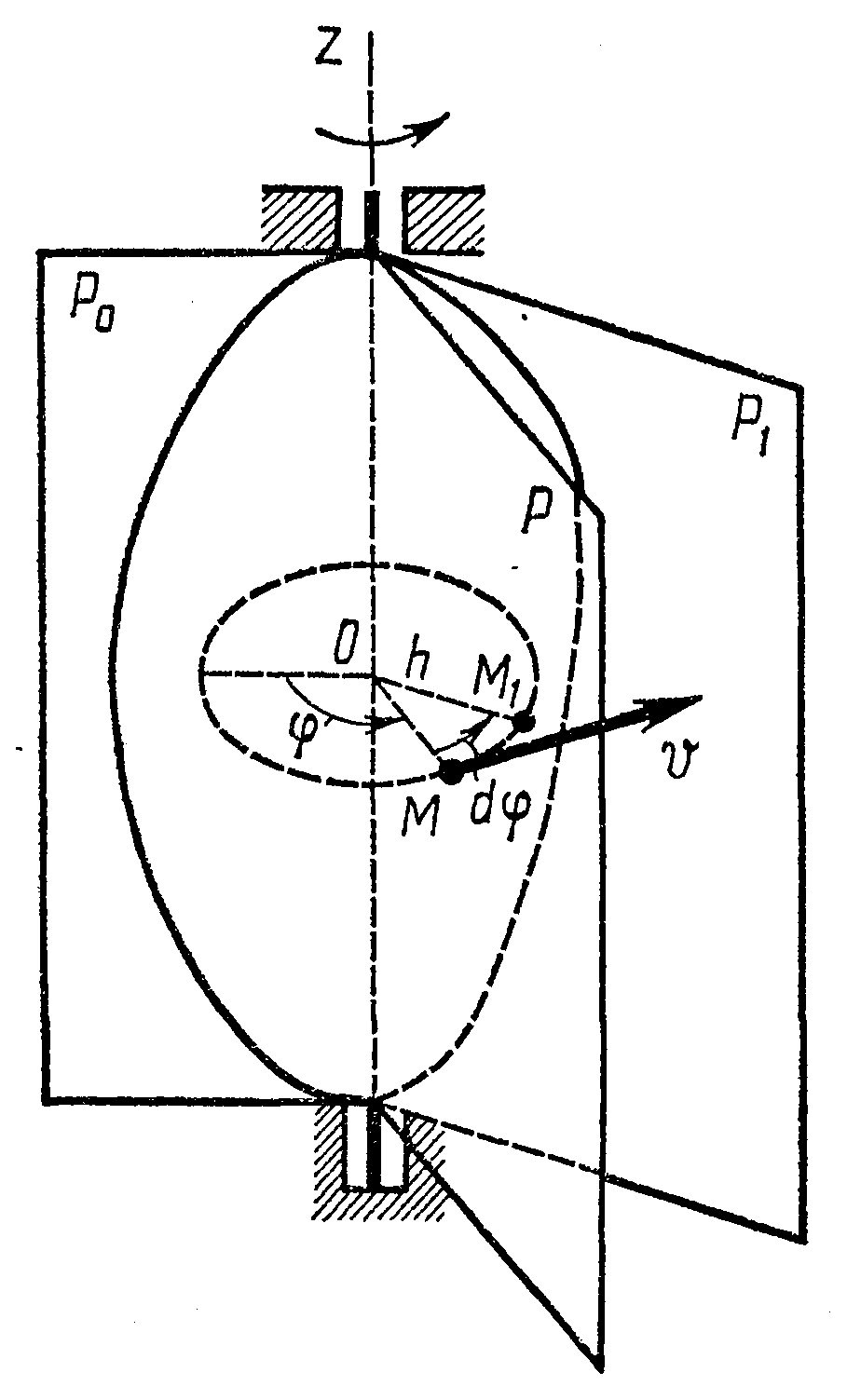 бозначим путь ММ₁ = dS

OМ₁ = OM = h

Модуль скорости точки:

ω – угловая скорость.

Модуль вращательной скорости точки равен произведению абсолютной величины угловой скорости тела на расстояние от точки до оси вращения.

Касательное ускорениеточки вращающегося тела иначе называется вращательным ускорением, а нормальное — центростремительным.

где ρ– радиус кривизны траектории.

Модуль центростремительного ускорения равен произведению квадрата угловой скорости тела на расстояние от точки до оси вращения.При ускоренном вращении касательное ускорение a_t направлен в туже сторону, что и вектор ϑ.

Центростремительное ускорение a_n направленно по нормали к поверхности к траектории в сторону вогнутости, т.е. к центру окружности, описываемого точкой. Полный модуль ускорения: