79. Статический момент площади.

80. Полярный момент инерции.

С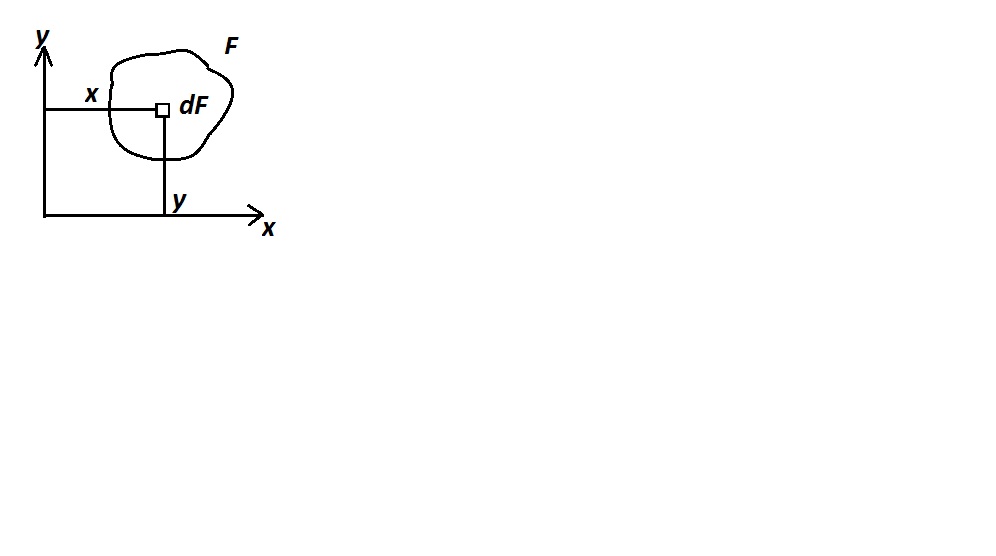 татистическим моментом площади плоской фигуры в этой плоскости наз. взятая по всей площади сумма произведений площадей.

S_x=∫ydF S_y=∫xdF

S_x=y_cF S_y=x_cF

СМП может быть положительный, отрицательный и равный нулю.

СМП отн-но оси, проходящей через центр тяжести, равен нулю.

При определении СМП сложной фигуры применяется метод разбиения, тогда СМР равен:

Полярным моментом инерции плоской фигуры отн-но полюса,леж. на этой же плоскости наз. взятая по всей площади сумма произведений площадей элементарных площадок на квадраты их расстояний до полюса.

81. Кручение круглого цилиндра.

Кручение – вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент. Момент пар наз. вращающимся.

Рассмотрим кручение круглого цилиндра

Ось цилиндра (ось кручения) осталась прямолинейной.

2.Диаметры окружностеё, нанесённыхна пов-ти цилиндра останутся неизменны и между ними не изменятся расстояния.

3.Образующие цилиндра превратятся в винтовые линии.

Вывод: при кручении круглого цилиндра справедлива гипотеза сечений,и также предполагается что R окружности остаются при деформации прямыми, т.к. в поперечном сечении бруса нет продольных сил, а расстояние между сечениями не изменяется. Т.о. деформация круглого стержня заключается в повороте поперечных сечений отн-но друг друга вокруг оси кручения. Причём угол поворота не прямо пропорционален от закреплённого сечения.

Угол поворота сечения равен углу части цилиндра, заключённой между данными сечениями и защемлением

При кручении возникает деформация сдвига, но не за счёт постоянного движения, а в результате вращающего движения.

При кручении в поперечных сечениях возникают только касательные внутренние силы, образующие крутящий момент.Крутящий момент – результирующий момент отн-но оси бруса, внутренних касательных сил, действующих в поперечном сечении

82. Напряжения и деформации при кручении.

Представим себе, что прямой круговой цилиндр, подвергаемый деформации кручения, состоит из бесконечно большого количества волокон, параллельных оси. Полагаем, что при кручении справедлива гипотеза о ненадавливании волокон.

Зная, что при кручении происходит деформация сдвига, естественно считать, что в точках поперечного сечения бруса возникают только касательные напряжения τ, перпендикулярные радиусу, соединяющему эти точки с осью кручения. Существование нормальных напряжений в продольном сечении исключено, так как справедлива гипотеза о ненадавливании волокон; нормальные напряжения в поперечном сечении не возникают, так как нет продольной силы.

Абсолютный сдвиг сечения волокна а равен дуге аа₁,а сечения волокна b-дуге bb₁.

где φ — полный угол закручивания, рад; r— радиус цилиндра; ρ — расстояние волокна b от оси кручения.

Так как радиусы сечения при кручении остаются прямыми, то величина абсолютного сдвига сечения волокон прямо пропорциональна их расстоянию от оси кручения.

Относительный сдвиг сечения волокна b:

• Применим формулу закона Гука при сдвиге:

При ρ=0 τ= 0, т. е. на оси кручения касательные напряжения равны нулю.

При ρ=r, τ= τ_тах, т. е. касательные напряжения достигают максимального значения у волокон, наиболее удаленных от оси кручения:

Т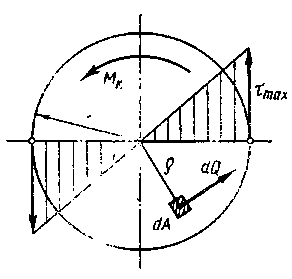 ак как относительный угол закручивания φ₀ есть величина постоянная для данного цилиндрического бруса, то касательные напряжения при кручении прямо пропорциональны расстоянию точек от оси кручения. Эпюра распределения напряжений вдоль радиуса сечения имеет вид треугольника.

Если брус состоит из одного участка, т. е. имеет постоянное сечение и постоянный по длине крутящий момент, то касательные напряжения в данном волокне будут по всей длине цилиндра одинаковы.