35.Давление газа на стенку сосуда. Основное уравнение Мкт идеального газа

Идеальный газ. Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. В модели идеального газа предполагается следующее: молекулы обладают пренебрежимо малым объемом по сравнению с объемом сосуда, между молекулами не действуют силы притяжения, при соударениях молекул друг с другом и со стенками сосуда действуют силы отталкивания.

Давление идеального газа. Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение явления давления газа на стенки сосуда.

   Качественное объяснение давления газа заключается в том, что молекулы идеального газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела. При столкновении молекулы со стенкой сосуда проекция  вектора скорости на ось ОХ, перпендикулярную стенке, изменяет свой знак на противоположный, но остается постоянной по модулю (рис. 82).

Поэтому в результате столкновения молекулы со стенкой проекция ее импульса на ось ОХизменяется от   до  . Изменение импульса молекулы показывает, что на нее при столкновении действует сила , направленная от стенки. Изменение импульса молекулы равно импульсу силы  :

 .

Во время столкновения молекула действует на стенку с силой  , равной по третьему закону Ньютона силе   по модулю и направленной противоположно. 

   Молекул газа очень много, и удары их о стенку следуют один за другим с очень большой частотой. Среднее значение геометрической суммы сил, действующих со стороны отдельных молекул при их столкновениях со стенкой сосуда, и является силой давления газа. Давление газа равно отношению модуля силы давления   к площади стенки S:

.

На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяло вычислить давление газа, если известны массаm0 молекулы газа, среднее значение квадрата скорости молекул   и концентрация nмолекул:

 . (24.1)

Уравнение (24.1) называют основным уравнением молекулярно-кинетической теории.    Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа  :

,

получим

 . (24.2)

Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

1. Средняя длина свободного пробега молекул.

Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями.

За секунду молекула в среднем проходит расстояние, численно равное ее средней скорости  Если за это же время она испытает в среднем   столкновений с другими молекулами, то ее средняя длина свободного пробега   , очевидно, будет равна

(3.1.1) Предположим, что все молекулы, кроме рассматриваемой, неподвижны. Молекулы будем считать шарами с диаметром d. Столкновения будут происходить всякий раз, когда центр неподвижной молекулы окажется на расстоянии меньшем или равном d от прямой, вдоль которой двигается центр рассматриваемой молекулы. При столкновениях молекула изменяет направление своего движения и затем движется прямолинейно до следующего столкновения. Поэтому центр движущейся молекулы ввиду столкновений движется по ломаной линии (рис. 1).

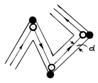
Молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметром 2d. За секунду молекула проходит путь, равный   . Поэтому число происходящих за это время столкновений равно числу молекул, центры которых попадают внутрь ломаного цилиндра, имеющего суммарную длину   и радиус d. Его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным   Если в единице объема газа находится n молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно (3.1.2)

В действительности движутся все молекулы. Поэтому число столкновений за одну секунду будет несколько большим полученной величины, так как вследствие движения окружающих молекул рассматриваемая молекула испытала бы некоторое число соударений даже в том случае, если бы она сама оставалась неподвижной.

Предположение о неподвижности всех молекул, с которыми сталкивается рассматриваемая молекула, будет снято, если в формулу (3.1.2) вместо средней скорости   представить среднюю скорость относительного движения  рассматриваемой молекулы. В самом деле, если налетающая молекула движется со средней относительной скоростью   , то молекула, с которой она сталкивается, оказывается покоящейся, что и предполагалось при получении формулы (3.1.2). Поэтому формулу (3.1.2) следует написать в виде:

(3.1.3)

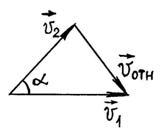
Предположим, что скорости молекул до столкновения были   и  Тогда   Из треугольника скоростей имеем (рис. 2)

Так как углы   и скорости   и   , с которыми сталкиваются молекулы, очевидно, являются независимыми случайными величинами, то среднее

от произведения этих величин равно произведению их средних. Поэтому

(3.1.5)

С учетом последнего равенства формулу (3.1.4) можно переписать в виде:

(3.1.6)

так как Cредняя квадратичная скорость пропорциональна средней скорости,

(3.1.7)

т. е.

Поэтому соотношение (3.1.6) можно представить так:

(3.1.8)

С учетом последнего выражения формула для средней длины свободного пробега приобретает вид:

(3.1.9)

Для идеального газа  Поэтому

(3.1.10)

Отсюда видно, что при изотермическом расширении (сжатии) средняя длина свободного пробега растет (убывает).

Как было отмечено во введении, эффективный диаметр молекул убывает с ростом температуры. Поэтому при заданной концентрации молекул средняя длина свободного пробега увеличивается с ростом температуры.

Вычисление средней длины свободного пробега для азота (d = 3•10-10 м), находящегося при нормальных условиях (р = 1,01•105 Па, Т = 273,15 К) дает:  , а для числа столкновений за одну секунду:   . Таким образом, средняя длина свободного пробега молекул при нормальных условиях составляет доли микрон, а число столкновений – несколько миллиардов в секунду. Поэтому процессы выравнивания температур (теплопроводность), скоростей движения слоев газа (вязкое трение) и концентраций (диффузия) являются достаточно медленными, что подтверждается опытом.