18. Раскройте сущность относительных величин, формы выражения. Относительные величины выполнения плана и планового задания, приведите методы их расчета.

Относительные статистические величины – обобщающие показатели, выражающие количественные соо-ия размеров социально-экономических явлений и процессов.

Их получают путем деления одной величины на другую. Величина с которой сравнивают знаменатель называется базой сравнения или основанием, а сравнимая величина – числитель текущей или отчетной.

Относительные величины, получаемые при сопоставлении абсолютных показателей называются относительными величинами первого порядка, а получаемые при сопоставлении др. величин величинами 2-го порядка.

Единицей измерения относительных величин зависят от того какие величины участвуют при сопоставлении.

19. Приведите методы расчета относительных величин : динамики, сравнения, интенсивности, структуры, координации

выделяют методы расчета относительных величин.

1) Относительные величины динамики (ig) – статистические величины характеризующие степени развития изучаемого явления во времени (темп роста)

2) Относительные величины структуры (di) – соотношение размеров отдельных частей сов-ти (mi) и всей сов-ти в целом сумма mi

Di=mi/сумма mi данная величина характеризует состав сов-ти и показывает, какую долю (предельный вес) во всей сов-ти составляют отдельные ее части.

3) относительные величины координации (ik) – отношение отдельных частей целого, между собой одна из частей применяется за базу.

4) Относительные величины интенсивности (iu) показатели характеризующие степень распространения или развития того или иного явления в определенной среде

5) Относительные величины сравнения (ic) соотношения одноименных статистических величин, относящихся и разным объектом или разным территориям.

20. Сущность средних величин

Средняя величина - обобщающая характеристика однородной сов-ти, явлений по определенному признаку.

Условия применения средних величин:

1) Качественная однородность изучаемой сов-ти

2) Сов-ть должна включать большое число факторов, так как только в этом случае колебание признака под влиянием случайных факторов взаимопогашаются и среднеустойчиво характеризует типичный уровень показателя в совокупности

В случае неоднородности сов-ти необходимо сгруппировать ее в однородные группы и по каждой из них определить среднюю величину.

Средняя величина используется в планировании, при анализе выполнения плана, в расчетах экономической эффективности производства и т.д.

Средняя рассчитанная по сов-ти в целом называется общей средней, а по каждой группе – групповой средней

Различают степенные средние (среднеорифметическая, среднегеометрическая, среднеагрегатная) и структурные средние

21.Охар-ть технику исчисления и область применения средней арифметической и средней гармонической

В статистике применяются различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя хронологическая средняя квадратическая и средняя кубическая.

Наиболее распространенным видом средних величин является средняя арифметическая. Она рассчитывается в двух формах – простой и взвешенной.

Средняя арифметическая простая называется так потому, что в основе ее вычисления лежит простое суммирование. Чтобы определить ее, все показатели варьирующего признака суммируются и делятся на их количество.

Формула средней арифметической простой:

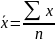
Где: х – варианты; n – число вариант.

Формула средней арифметической взвешенной:

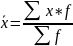
Где: х – варианты; f – веса.

Эта средняя называется взвешенной потому, что для ее определения значения признака, по которым эта средняя исчисляется, не просто складываются, а предварительно умножаются на частоту (взвешиваются).

Применяется эта средняя в том случае, если показатели в совокупности встречаются несколько раз (т.е. повторяются). Иногда среднюю арифметическую величину исчисляют по данным интервального вариационного ряда (когда варианты представлены в виде интервалов «от – до»). Для исчисления средней нужно прежде всего получить середину интервала каждой группы, а затем расчет производится по формуле арифметической взвешенной.

Средняя гармоническая взвешенная рассчитывается по формуле:

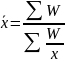
Где: х – варианты; W – объем признака.

Средняя гармоническая применяется в тех случаях, когда отсутствует показатель частоты. Она представляет собой величину обратную средней арифметической из обратных значений признака