3. Игра – математическая модель антогонистической ситуации

Игрой называется математическая модель конфликтной ситуации. Раздел теории исследований операций, занимающейся математическими моделями принятия оптимальных решений в условиях конфликта, называется теорией игр.

Заинтересованные стороны в игре называются игроками. Любое возможное в игре действие игрока называется его чистой стратегией.

Игра называется конечной, если множество стратегий каждого игрока конечно.

Чаще степень удовлетворения интересов игрока А характеризуется его функцией выигрыша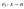 , определенной на множестве всех ситуаций и ставящий в соответствие каждой ситуации некоторое число , называемое выигрышем игрока А в ситуации x.

Аналогично, для игрока В функция выигрыша 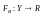определена на множестве ситуаций 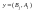и каждый из них ставит в соответствие число , называемое выигрышем игрока В в ситуации y.

Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявления для каждого из них «оптимальных стратегий».

Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или эквивалентно минимальный возможный средний проигрыш). Выбор оптимальной стратегии базируется на принципе, предполагающем, что оба игрока разумны в одинаковой степени и поведение каждого из них направлено на противодействие противнику в достижении его цели. Таким образом, теория игр абстрагируется от ошибок, просчетов, азарта и риска, присущих игрокам в реальных случаях.

Если в парной игре игроки преследуют противоположные цели, то игра называется антагонистической. В такой игре один из игроков выигрывает ровно столько, сколько проигрывает другой. Поэтому, функции выигрышей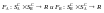 соответственно игроков А и В связаны между собой соотношением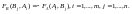 Из этого равенства следует, что и потому антагонистические игры называют играми двух сторон с нулевой суммой выигрыша.

В силу равенства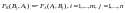 функция выигрыша игрока В полностью определяется функцией выигрыша игрока А и, следовательно, антагонистическая игра с игроками А и В определяется совокупностью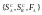 , состоящей из множества чистых стратегий игрока А, множества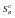 чистых стратегий игрока В и функции выигрыша игрока А.

В конечной антагонистической игре с игроками А и В можно строки некоторой матрицы поставить в соответствие стратегиям игрока А, а столбцы – в соответствие стратегиям игрока В. Если на пересечениях строк и столбцов расставить значения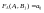 функции выигрыша игрока А, соответствующие ситуации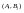 , то получим матрицу А, которая называется матрицей выигрышей игрока А.

Аналогичным образом, из значений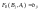 функции выигрыша игрока В, можно составить матрицу В выигрышей игрока В. В силу равенства . Таким образом, матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей выигрышей и в силу этого называется матричной.

4. Классификация игр по различным признакам

Теория игр- теоритич основы математич моделей принятия оптим реш-й в конфликт ситуациях рыночн отнош-й.

Конфликт ситуация-это столкновение интересов не менее 2 сторон,каждая из кот для достижения целей имеет возможн действов разл способами в зависимости от действ противоборств сторон.

Игрой называется упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилам.

Коалиция -объединение игроков по различным причинам.

Правила игры- система условий с целью формализаций:

а)стратегий игроков

б)объем информ,кот каждый из игроков может получить от действ. др. игрока

в)исход игры в рез-те любой совокупной стратегии игроков.

Исход игры-набор ситуаций,образующийся в рез-те определенного хода(выбора стратегии) каждым из игроков в условиях конфликта.

Стратегии-существование определенных возможных действий у каждого из игроков.

Функ выигрыша игрока А→F_A-это степень удовлетвор интересов игрока А.

F_A: X→R, X= . F_A(x)ЄR

Для игрока В-аналогично. F_B-фун-я выигрыша игрока В.

F_B: Y→R, Y= 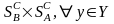, F_B(y)ЄR.

Игры можно классифицировать по различным признакам:

· по числу «игроков» (сторон)-множественные ( ≥2) и парные;

· по числу ходов в игре:

многошаговые;

бесконечные;

· математической структуре модели игры:

рекурсивные;

дифференциальные;

· по числу стратегий игры:

конечные;

бесконечные, если хотя бы у одного «игрока» число стратегий бесконечно;

· по взаимоотношениям игроков:

кооперативные (коалиционные), в которых принимающие решение игроки объединены в фиксированные коалиции; члены одной коалиции могут свободно обмениваться информацией и принимать полностью согласованные решения; игроки могут вступать в коалицию и договариваться о совместных действиях

бескоалиционные, в которых каждая коалиция или множество игроков, действующих совместно, состоит лишь из одного игрока;

· по степени информативности «игроков» в игре:

детерминированные, когда условия, в которых принимаются решения, известны полностью;

стохастические, когда известно множество возможных вариантов условий и их вероятностное распределение;

неопределенные, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях;

· по выигрышу игры:

антагонистические;

игры с ненулевой суммой;

· по характеру получения информации:

статические игры или игры в нормальной форме (игроки получают всю предназначенную им информацию до начала игры и ходят один раз, одновременно и независимо);

динамические игры или игры в позиционной форме (информация поступает игрокам в процессе развития игры);

· по полноте имеющейся у игроков информации:

статические игры с полной информацией

статические игры с неполной информацией);

динамические игры с полной информацией и неполной информацией

Игры классифицируются по различным признакам.

Если в игре образование коалиций недопустимо или нецелесообразно, такие игры называют бескоалиционными, однако бескоалиционными можно считать и игры, в которых совокупности коалиций действия и коалиции интересов совпадают. Бескоалиционная игра представляет собой совокупность множества игроков, множеств их стратегий и наборов их функций выигрыша. С таких играх основная цель игрока – получение выигрыша. Если даже игроки объединяются в коалиции, основная задача игры состоит в дележе общего выигрыша между игроками.

В коалиционных играх совокупности коалиций действий и коалиций интересов различны. В коалиционных играх игроки стремятся максимизировать выигрыши коалиций без последующего их распределения между игроками.

Игры можно классифицировать по числу игроков: парные и множественные. Если в парной игре игроки преследуют противоположные цели, игра называется антагонистической. В такой игре один из игроков выигрывает ровно столько, сколько проигрывает другой. F_A= - F_B. Такие игры также называют играми с нулевой суммой. Антагонистическая игра с игроками А и В вполне определяется совокупностью {S_A^C, S_В^C, F_A}.

Если множество стратегий каждого игрока конечно, то игра конечна. В противном случае она называется бесконечной. В конечной антагонистической игре с игроками А и В можно строки некоторой матрицы поставить в соответствие стратегиям А_i игрока А , а столбцы – в соответствие стратегиям В_J игрокам В. Если на пересечениях столбцов и строк расставить значения F_A(А_i, В_J)=а_ij функции выигрыша игрока А, соответствующие ситуации (А_i, В_J), то получим матрицу А, которая называется матрицей выигрышей игрока А. Аналогично для игрока В.

В силу равенства В= - А^Т. Матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей и называется матричной.

Если в конечной бескоалиционной игре участвуют 2 игрока А и В с различными, но не противоположными интересами, то матрицы их выигрышей А и В уже не будут удовлетворять условию В= - А^Т, и потому такую игру называют биматричной. Она задается совокупностью {S_A^C, S_В^C, А, В}.