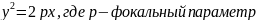11.Плоскость. Взаимное расположение плоскостей. Расстояние от точки до плоскости.

Пусть плоскость проходит через точку M₀ (x₀, y₀, z₀) и перпендикулярна вектору  (M, N, L). Вектор  (M, N, L) называется вектором нормали к плоскости.

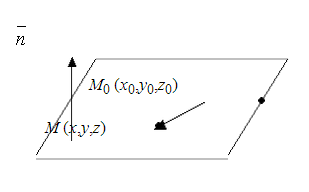
Нормальный вектор-вектор, который перпендикулярен к плоскости.

Уравнение Ax+By+Cz+D=0 называется общим уравнением плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.

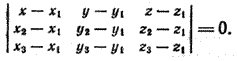
Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.

Двугранный угол между плоскостями равен углу образованному прямыми L1 & L2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.

cos α  =	|A1·A2 + B1·B2 + C1·C2|
	(A12 + B12 + C12)1/2(A22 + B22 + C22)1/2

Если заданы уравнения плоскостей A₁ & A₂,то угол между плоскостями можно найти, используя следующую формулу

Условие параллельности плоскостей имеет вид:

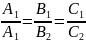
Условие совпадения плоскостей:

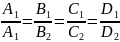
Условие перпендикулярности плоскостей:

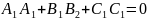
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

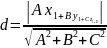
12.Прямая в пространстве. Взаимное расположение двух прямых в пространстве.

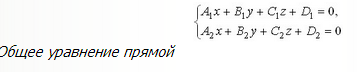
Пример:

13. Прямая и плоскость в пространстве. Взаимное расположение прямой и плоскости.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

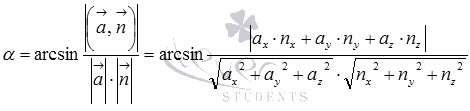
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

            Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

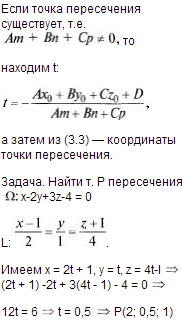
14. Общее уравнение поверхности второго порядка. Поверхности вращения. Конические поверхности. Цилиндрические поверхности.

Общее уравнение поверхности 2 порядка:

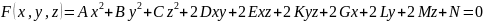
Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Поверхности вращения-окружность, коническая, сфера, цилиндрическая, (эллиптический, гиперболический, параболический), тор, , параболоид вращения, однополостный гиперболоид вращения , двуполостный гиперболоид вращения(1)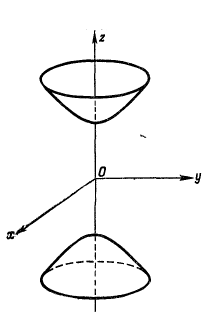 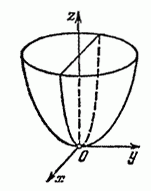-эллиптический параболоид

Конической поверхностью называется поверхность , образованная прямыми (образующими конуса), проходящими через данную точку (вершину конуса) и пересекающими данную линию (направляющую конуса).

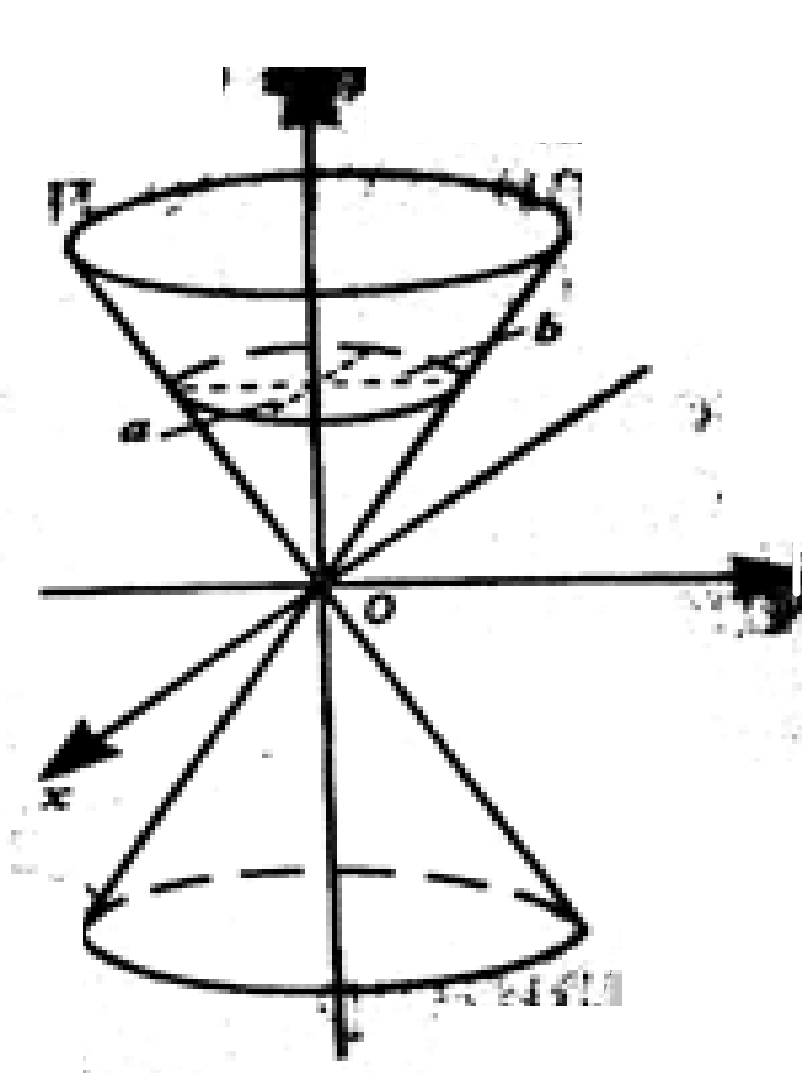
Цилиндрическая поверхность — поверхность второго порядка, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.

Эллиптический цилиндр: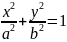

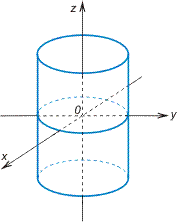
Гиперболический цилиндр: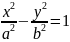

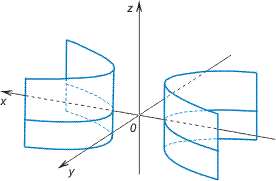
Параболический цилиндр: