27)Определение функции комплексного переменного и её геометрический смысл

Пусть Д некоторое мн-во компл. чисел. Однозначной функцией компл. переменного наз-ся правило по которому компл. числу z соответствует единственное компл. число w. Такое соответствие обознач. w=f(z) или f :w - >z. Мн-во Д наз-ся мн-вом определения функции f. Если обозначить z=x+iy, w=u+iv, то задание функции w=f(z) компл. переменного равносильно заданию на том же мн-ве 2-х функций действ. переменных х и у, принимающих действ. значения u=u(x,y) и v=v(x,y). Наряду с плоскостью z=x+iy рассмотрим также плоскость компл. переменного w=u+iv с координатами (u,v). Когда т. z пробегает мн-во Д на плоскости переменного z соответственно т. w пробегает другое

мн-во Е. Т.о. однозначная ф-ция w=f(z) отображает мн-во Д на мн-во Е, т.е. каждой т. z из Д ставим в соответствие точку w из Е. Точка w наз-ся образом точки z, а т. z прообразом т. w при отображении w=f(z).

28. Предел функции комплексного переменного

Введем понятие предела функции w=f(z) в точке. Пусть задана т. z₀ из С и δ>0. Проколотой δ- окрестностью

т. z₀=0 наз-ся δ-окрестность этой точки за исключением самой т. z₀ , т.е. внутренность круга радиуса δ с центром z₀ из которого удален центр z₀. Это мн-во можно записать в виде 0<| z-z₀ |<δ. Пусть функция w=f(z) определена в некоторой проколотой окрестности т z₀. Число А наз-ся пределом функции w=f(z) в т. z₀ , если для любого ε>0 найдется такое δ>0, δ=δ(ε), что для всех точек проколотой окрестности т. z₀ выполняется неравенство |f(z)-A|<ε. Наличие у функции f(z) предела в точке А записывается в виде

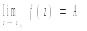
и означает следующее: для любой окрестности U_A т. А найдется такая проколотая окрестность т. z₀ , что для всех точек z проколотой окрестности соответствующее значение f(z) лежит в U_A . В такой форме определение предела охватывает и случай z=∞ и А=∞. Под проколотой окрестностью т. z=∞ понимается мн-во |z|>R. Данное определение предела для функции аналогично опред-нию предела для функции действ. переменных. Поэтому важные теоремы сохраняют силу и для фуции компл. переменного. Если функция f(z) определена лишь в области Д , то для граничной точки z₁ не существует проколотой окрестности, в которой задано значение f(z) . Число А наз-ся пределом функции w=f(z) в граничной точке z₁, если для любого ε>0 найдется такое δ>0, что для всех точек проколотой δ-окрестности точки z₁ принадлежащей области Д выполняется неравенство

|f(z)-A|<ε.

29)Непрерывность функций комплексного переменного.

Наличие у функции f(z) предела в точке А записывается в виде

и означает следующее: для любой окрестности U_A т. А найдется такая проколотая окрестность т. z₀ , что для всех точек z проколотой окрестности соответствующее значение f(z) лежит в U_A . В такой форме определение предела охватывает и случай z=∞ и А=∞. Под проколотой окрестностью т. z=∞ понимается мн-во |z|>R. Данное определение предела для функции аналогично опред-нию предела для функции действ. переменных. Поэтому важные теоремы сохраняют силу и для фуции компл. переменного. Если функция f(z) определена лишь в области Д , то для граничной точки z₁ не существует проколотой окрестности, в которой задано значение f(z) . Число А наз-ся пределом функции w=f(z) в граничной точке z₁, если для любого ε>0 найдется такое δ>0, что для всех точек проколотой δ-окрестности точки z₁ принадлежащей области Д выполняется неравенство |f(z)-A|<ε. Функция w=f(z), определенная в окрестности (не проколотой!) точки z₀ наз-ся непрерывной в т. z₀, если

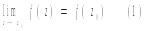
Непрерывность функции w=f(z)=u(x,y)+iv(x,y) в т. z₀=x₀+iy₀ эквивалентна непрерывности двух действ-ных функций u(x,y) и v(x,y) двух действ. переменных х и у в т. (x₀,y₀). Функция w=f(z) , определенная в области Д наз-ся непр-ной в этой области, если f(z) непрерывна в каждой точке области Д. Функция w=f(z) наз-ся непр-ой в замкнутой области Д', если она определена в Д' и для каждой т. z₀ из Д выполнено равенство (1). Зафиксируем т. z₀ и возьмем другую т. z из Д. Тем самым аргумент изменяется на величину ∆z=z-z₀=∆x+i∆y, наз-ся приращением аргумента. Соотв-щее изменение функции ∆w=f(x)-f(z₀)=∆u+i∆v наз-ся приращением.