21.Гипотезы ошибки первого и второго рода.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода принято обозначать через  ; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0.05 или 0.01. Если, например, принят уровень значимости, равный 0.05, то это означает, что в пяти случаях из ста мы рискуем допустить ошибку первого рода (отвергнуть правильную гипотезу).

Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины – критерия согласия.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

   

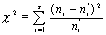
22-23.Введение понятия комплексного числа. Представление комплексного числа на плоскости.

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы  , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:

.

(1)

В литературе часто мнимую единицу обозначают через  . Тогда комплексное число  можно представить в виде:

,

(2)

где   носит название действительной части или реальной части и обозначается  , а  носит название мнимой части и обозначается как  . Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.

Рисунок 1: Представление комплексного числа на плоскости

Комплексная плоскость   делится прямыми реальной части   (прямой действительных чисел) и прямой мнимых чисел  на четыре четверти. Любое комплексное число   ,будет представляться точкой на комплексной плоскости с координатами   и  . Если число не содержит мнимой части, то оно действительное и находится на прямой , а если число не содержит реальной части, то оно называется чисто мнимым и находится на оси  .

24. Откры́тое мно́жество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии.

25.За́мкнутое мно́жество — подмножество пространства, дополнение к которому открыто.

Определение

Пусть дано топологическое пространство  . Множество   называется замкнутым относительно топологии  , если существует открытое множество   такое что  .

26)Сфера Римана. Расширенная комплексная плоскость.Риман предложил другую геометрическую интерпретацию множества комплексных чисел, – он расположил их на сфере, которая и получила название сферы Римана.

Наиболее просто показать, как каждому комплексному числу ставится в соответствие точка сферы, это расположить сферу "южным полюсом" на начало координат комплексной плоскости, а из "северного полюса" провести лучи в каждую точку плоскости. Точку, в которой луч, идущий

к числу z, пересечёт сферу, мы и назовём точкой z.