8. Схема Бернулли

Проводятся опытов, в каждом из которых может произойти определенное событие («успех») с вероятностью (или не произойти — «неудача» — ). Задача — найти вероятность получения успехов в опыте.

Решение:

Количество успехов — величина случайная, которая имеет распределение Бернулли.

9. Локальная теорема Лапласа: Если вероятность появления события в каждом из независимых испытаний равна одной и той же постоянной то вероятность того, что во всех этих испытаниях событие  появится ровно  раз, приближенно вычисляется формулой:

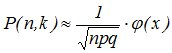
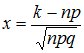
Интегральная: Пусть вероятность появления события А в каждом из n (n→∞)независимых испытаний равна одной и той же постоянной р (0<р<1), то вероятность   того, что во всех этих испытаниях событие А появится не менее k₁ и не более k₂ раз, приближенно вычисляется формулой:

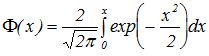
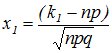
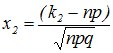
10. Случайные величины.

Случайные величины – величины, которые в результате испытания получает 1 и только 1 значение ( неизвестное).

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически

11. Биноминальное распределение. Распределение Пуассона.

Биноминальное распределение: Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях.

P(x=k)=

Распределение Пуассона: Случайное число событий, происшедших за время от 0 до Т, распределено по закону Пуассона с параметром l=аТ, где а>0 – параметр задачи, отражающий среднюю частоту событий. Вероятность k покупок в течение большого интервала времени, (например, – дня) составит

P(Z=k)=

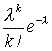
12. Поток событий и его свойства.

Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в какие-то моменты времени.

• Свойство стационарности: вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета.

• Свойство отсутствия последействия: вероятность появления k на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.

• Свойство ординарности: вероятностью наступления за элементарный промежуток времени более одного события можно пренебречь по сравнению с вероятностью наступления за этот промежуток не более одного события

13. Математическое ожидание. Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей. Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания.

14. Теорема Бернулли. Бернулли: Если в каждом из п независимых опытов вероятностьр появления события А постоянна, то при достаточно большом числе испытаний вероят-ность того, что модуль отклонения относительной частоты появлений А в п опытах от р будет сколь угодно малым, как угодно близка к 1:

Плотность распределения вероятности. Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.

15. Непрерывное равномерное распределение.Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины. Непрерывная случайная величина Х равномерно распределена в интервале [а; в], если ее плотность вероятности в этом интервале постоянна, т.е. если все значения в этом интервале равновероятны:

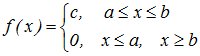
16. Нормальное распределение.

Нормальное распределение, также называемое гауссовым распределением, гауссианой илираспределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

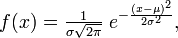
17. Система случайных величин.

Существуют также случайные величины, которые определяются двумя, тремя и т.д. числами. Такие случайные величины называются двумерными, трехмерными и т.д. В зависимости от типа, входящих в систему случайных величин, системы могут быть дискретными, непрерывными или смешанными, если в систему входят различные типы случайных величин. Определение. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.  Определение. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.

18. Генеральная совокупность, генеральная выборка (от лат. generis — общий, родовой)(в англ. терминологии — population) — совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.

Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность - это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, женщины 10-89 лет, использующие крем для рук определённых марок не реже раза в неделю, и имеющие доход не ниже $150 на одного члена семьи.

19. Смещенная и несмещенная оценки.

Несмещённая оце́нка в математической статистике — это точечная оценка, математическое ожидание которой равно оцениваемому параметру. Смещенная оценка - статистическая оценка, математич. ожидание к-рой не совпадает с оцениваемой величиной. 

20. Доверительный интервал.

Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

20.Точность оценки, доверительная вероятность, доверительный интервал. 

Доверительный интер-вал для оценки мат ожидания нормального рас-пределения при известном мат ожидании (вы-вод). Точечные оценки неизвестного параметра Ө хороши в качестве первоначальных результа-тов обработки наблюдений, их недостаток в том, что неизвестно с какой целью они дают оценоч-ный параметр. Для выбора небольшого объема вопрос о точности существенен, т.к. между Ө и Ө* м. б. большое расхождение, кроме того, при решении задач часто требуется определить и надежность этих оценок, тогда и возникает зада-ча о приближении параметра Ө не 1 числом, а целым интервалом (Ө1*;Ө*