63. Скалярные и векторные поля.
-
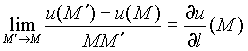определение производной функции
(скалярного поля) и(М) в точке М по
направлению 
.
-
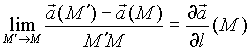определение производной вектор-функции
(векторного поля) 
в
точке М по направлению l
Пусть
функция 
задана
в некоторой области пространства 
, 
.
Поверхность в пространстве
,
определённая уравнением 
,
где 
--
постоянная, называется поверхностью
уровня
функции
.
Если 
,
то множество, заданное уравнением 
,
называется линией
уровня.
64.
Оператор 
(16.1)
называется оператором Гамильтона или набла-оператором и обозначается символом s
(«набла»).
Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю:
.
Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю.
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля.
,
то
есть для сил потенциалом 
является 
.
Когда U не зависит от времени, оно является
потенциальной энергией, и тогда знак
«-» возникает просто по определению. В
противном случае знак сохраняется ради
единообразия
дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.
