56.Определение и вычисление криволинейного интеграла второго порядка.

Определение

Составим интегральную сумму функции f (x,y) по кривой L относительно

Пусть на ориентированной кривой L определены две функции f (x, y) и g (x, y). Тогда сумма интегралов (24) и (25) называется общим криволинейным интегралом 2-го рода от функций f (x,y) и g (x,y) по кривой L и обозначается

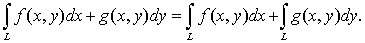
Вычисление криволинейного интеграла 2-го рода.

Пусть ориентированная кривая L задана параметрическими уравнениями x = j (t), y=y (t), a ≤ t ≤b, где j (t), y (t) - непрерывно дифференцируемые на отрезке [a, b ] функции. Тогда

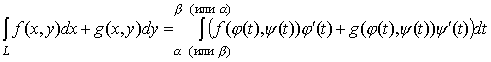(1)

57.Формула Грина. Условие независимости криволинейного интеграла второго рода от вида пути интегрирования.Пусть D - некоторая замкнутая область на плоскости хОу, ограниченная контуром L. На ней заданы функции Р = Р(х,у) и Q = Q(x,y), непрерывные на D вместе со своими частными производными первого порядка. Формула Грина связывает криволинейный интеграл второго рода по L с двойным интегралом по области D:

Движение по контуру L - в положительном направлении.С помощью формулы Грина значение криволинейного интеграла по замкнутому контуру можно найти, вычислив двойной интеграл

58. Определение поверхностного интеграла первого рода. Пусть в пространстве  переменных x,y,z задана кусочно-гладкая поверхность , на которой определена функция f(x,y,z). Разобьём поверхность на  частей , на каждой из частей  выберем произвольную точку , найдём  и площадь части  (которую будем обозначать тем же символом ), и составим интегральную сумму 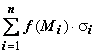. Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения поверхности   на части , ни от выбора точек , то функция f(x,y,z) называется интегрируемой по поверхности , а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности, и обозначается .

59. Поверхностный интеграл второго порядка.

Определение. Если при стремлении к нулю шага разбиения поверхности S интегральные суммы, составленные как суммы произведений значений некоторой функции на площадь частичной поверхности, имеют конечный предел, то этот предел называется поверхностным интегралом второго рода

60. Стокса формула

Стокса формула, формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности S, ограниченной контуром L. С. ф. имеет вид:

 ,

причём направление обхода контура L должно быть согласовано с ориентацией поверхности S. В векторной форме С. ф. приобретает вид:

 ,

где а = Pi + Qj + Rk, dr — элемент контура L, ds — элемент поверхности S, n — единичный вектор внешней нормали к этой поверхности. Физический смысл С. ф. состоит в том, что циркуляциявекторного поля по контуру L равна потоку вихря поля через поверхность S. С. ф. предложена Дж. Г.Стоксом в 1854.

61. Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля пообъёму, ограниченному этой поверхностью:

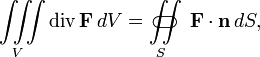
то есть интеграл от дивергенции векторного поля  , распространённый по некоторому объёму  , равен потоку вектора через поверхность  , ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.