51 Определение тройного интеграла и его свойства
Пусть
в замкнутой кубируемой области V
пространства XYZ задана
произвольная функция 
.
Разобьем область V на n областей 
не
имеющих общих внутренних точек. В каждой
точке области 
возьмем
произвольно точку 
.
Значение функции
в
точке 
умножим
на объем
i-й
области и сложим такие произведения по
всем областям деления. Полученная
сумма 
называется
интегральной суммой для функции
по
области V. Для функции
можно
составить бесчисленное множество
интегральных сумм по области V.
52 Основные свойства тройного интеграла
Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства:
,
где k - константа;
Если 
в
любой точке области U, то 
;
Если
область U является объединением двух
непересекающихся областей U1 и
U2,
то 
;
Пусть
m - наименьшее и M - наибольшее значение
непрерывной функции f (x,y,z) в области
U. Тогда для тройного интеграла справедлива
оценка: 
где
V - объем области интегрирования U.
Теорема
о среднем значении тройного интеграла.
Если функция f (x,y,z) непрерывна в
области U, то существует точка M0 
U,
такая, что 
где
V - объем области U.
53. Замена переменных в тройном интеграле. Якобиан. Цилиндрические, сферические координаты.
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
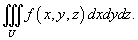
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
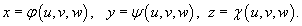
3.Якобиан преобразования I (u,v,w), равный
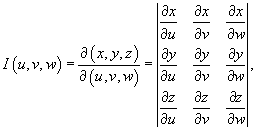
и он отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
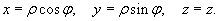
Здесь предполагается, что
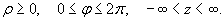
Якобиан перехода от декартовых координат к цилиндрическим равен
Тогда формула замены переменных при данном преобразовании имеет вид:
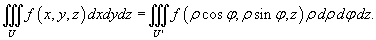
Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где
ρ − длина радиуса-вектора точки M;
φ − угол, образованный проекцией радиуса-вектора на плоскость Oxy и осью Ox;
θ − угол отклонения радиуса-вектора от положительного направления оси Oz (рисунок 1).
54.Вычисление координат центра тяжести и моментов инерции с помощью тройного интеграла
Для вычисления
координат центра тяжести тела
нужны статические моменты относительно
координатных плоскостей Оху, Охz, Оуz;
обозначим их соответственно
Формулы для
координат
центра тяжести неоднородного тела,
плотность которого задается функцией
занимающего область
:
Если тело однородно,
т. е.
,
то формулы упрощаются:
где
V-
объём тела.
55. Определение и вычисление криволинейного интеграла первого порядка.
Определение
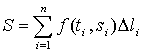
Предел
,
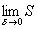если он существует, называется
криволинейным интегралом 1-го рода от
функции f (x,y) по кривой L и обозначается
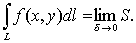
Вычисление криволинейного интеграла 1-го рода.
Пусть кривая L задана параметрическими уравнениями x = j (t), y= y (t), a ≤ t ≤b,
где j (t), y (t) - непрерывно дифференцируемые на отрезке [a, b ] функции. Тогда
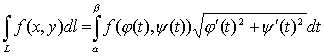
Пусть кривая L задана явно уравнением y = g (x), a≤ x ≤b, где g (x) -непрерывно дифференцируемая на [a, b] функция. Тогда
