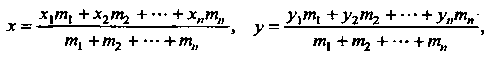39Формула Коши

П усть функция   аналитическая в односвязной замкнутой области   ( ), с кусочно-гладкой границей  , ориентированной в положительном направлении (рис. 142), т. е. против часовой стрелки. Тогда имеет место формула Коши

,

где   - любая точка внутри контура  .

Таким образом, аналитическую функцию достаточно определить на контуре  , а по формуле (1) можно автоматически получить ее значения в других точках  .

Производные высших порядков явно заданной функции

Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.

Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у"

Итак, у"=(у')'.

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'

Производной n-го порядка (или n-й производной) называется производная от производной  (n-1) порядка:

y⁽ⁿ⁾=(y^(n-1))¢ .

Производные порядка выше первого называются производными высших порядков.

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (у^ν или у⁽⁵⁾— производная пятого порядка).

40. Двойной интеграл.

Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных  z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как

где R - область интегрирования в плоскости Oxy

41.

42. Определение двойного интеграла.  Пусть на плоскости Oxyзадана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция .

Разобьём область D произвольным образом на  подобластей  (не имеющих общих внутренних точек). Символом  будем обозначать площадь области ; символом  здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D

43. Вторая теорема о среднем значении касается свойств интеграла от произведения двух функций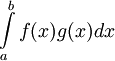 

Вторая теорема о среднем значении. Если функция f(x) монотонна (нестрого) на отрезке [a,b], а функция g(x) интегрируема на [a,b], то существует точка  такая, что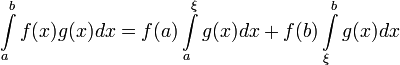 

44. Вычисление двойного интеграл водится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла.

45. Геометрическая интерпретация двойного интеграла

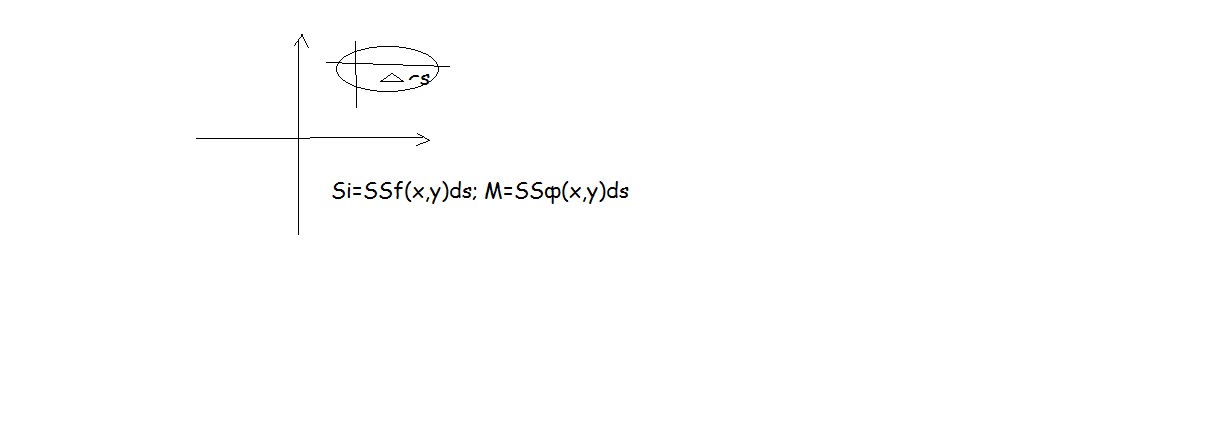
46. Замена переменных в решении двойного интеграла.

Для вычисления двойного интеграла   иногда удобнее перейти в другую систему координат.  Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.  В новой системе координат вычисление двойного интеграла значительно упрощается.  Замена переменных в двойном интеграле описывается формулой

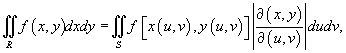
47. Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат.

Якобиан такого преобразования имеет вид

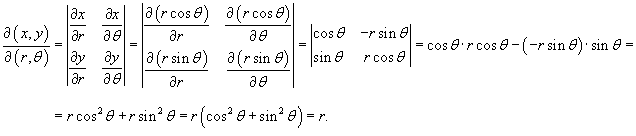
48. Интеграл Пуассона.

49. Вычисление площади поверхности с помощью двойного интеграла.

Пусть поверхность S определяется уравнением z = f (x, y). Поверхность S предполагается гладкой в каждой точке этой поверхности, то есть существует нормаль к поверхности в каждой её точке. Пусть D есть область определения функции на координатной плоскости Оху. Площадь поверхности над областью D вычисляется по формуле

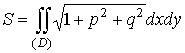
49. Вычисление площади поверхности с помощью двойного интеграла.

Пусть поверхность S определяется уравнением z = f (x, y). Поверхность S предполагается гладкой в каждой точке этой поверхности, то есть существует нормаль к поверхности в каждой её точке. Пусть D есть область определения функции на координатной плоскости Оху. Площадь поверхности над областью D вычисляется по формуле

49

Площадь поверхности тела вращения

Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

Тогда 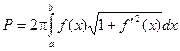  - формула вычисления Площади поверхности тела вращения.

50

Масса плоской фигуры

(  - плотность).

Центр тяжести системы масс

Дана система масс Помещенных соответственно в точках

Некоторой плоскости. Формулы, выражающие координаты центра тяжести этой системы масс, имеют вид