1.2. Интерференция световых волн.

Если монохроматические световые волны имеют посто­янную во времени разность фаз и колебания их световых векто­ров происходят в одной плоскости, то они называются коге­рентными (от греч. cohereus - согласованный). Явление перераспре­деления интенсивности световой волны в пространстве при на­ложении двух или нескольких когерентных волн называется ин­терференцией света.

Любое светящееся тело состоит из огромного количества светящихся атомов, каждый из которых излучает лишь очень короткое время τ = 10^- с и затем «потухает». За это время атом испускает кусок волны приблизительно 3 м, называемый волно­вым цугом. Затем возбуждение атома повторяется, но излучае­мый волновой цуг будет иметь другую начальную фазу, которая задается случайным образом. Следовательно, цуги одного атома, а тем более цуги разных атомов, принадлежащих одному источ­нику, будут некогерентными. По этой причине в результате на­ложения световых волн от двух независимых источников (на­пример, двух электрических ламп накаливания) явление интер­ференции никогда не наблюдается.

1.3. Интерференционная картина.

П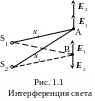 усть в некоторую точку А одновременно приходят две световые волны от когерентных источников света S₁ и S₂, свето­вые векторы которых колеблются в одной плоскости (рис. 1.1). Пусть источники начинают излучать одновременно, начальные фазы волн равны нулю и амплитуды одинаковы. Тогда уравнения волн можно записать следующим образом:

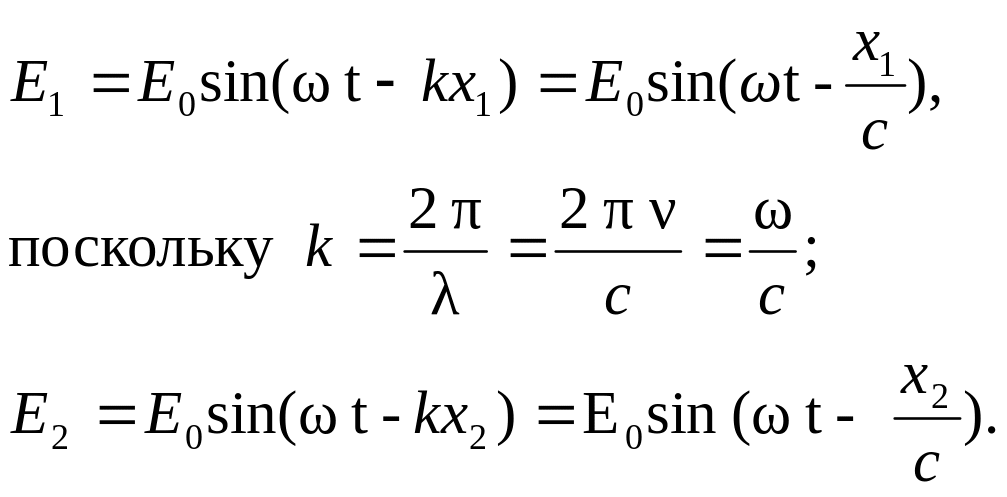
Складывая эти выражения, можно получить, что результирующая величина Е в точке А будет равна:

.

Величина не зависит от времени и является ам­плитудой суммарного колебания в точке А. Амплитуда может принимать нулевое значение, если а это выпол­няется если аргумент косинуса равен нечетному числу π/2. При этом происходит взаимное «гашение» волн и мы наблю­даем ослабление интенсивности суммарной волны, то есть ин­терференционный минимум. Определим положение в простран­стве таких точек:

, где m = 0, 1, 2…. - любое целое число, которое называется порядком интерференции, запись означает нечетное число. х₁ и х₂ – геометрические пути световых волн от источников света S₁ и S₂ соответственно, до произвольной точки А (рис. 1.1). Разность х₂ - х₁ = Δ называется геометрической разностью хода волн. Если свет распространя­ется в среде с показателем преломления n, необходимо рассмат­ривать оптический путь волн l = xn. Если световые волны про­ходят в разных средах, их оптические пути будут l₁=x₁n₁ и l₂=x₂n₂ и оптическая разность хода Δ = l₂ - l₁. Таким образом, если в произвольной точке пространства оптическая разность хода накладываемых волн равна нечетному числу полуволн, то в ней наблюдается минимум интерференции. Условие есть условие интерференционного минимума.

Если что возможно при равенстве аргу­мента нулю или четному числу π/2, амплитуда светового вектора для данной точки будет в любой момент времени равна 2Е₀. Определим положение этих точек:

.

Если в произвольной точке пространства оптическая раз­ность хода накладываемых волн равна четному числу полуволн или целому числу длин волн, то в ней наблюдается максимум интерференции и условие является усло­вием интерференционного максимума. Если между световыми волнами существует разность хода, то они также обладают раз­ностью фаз.

Получим условия интерференционных максимумов и ми­нимумов для разности фаз δ:

.

Если вместо Δ подставить значения Δ_max и Δ _min, то мы по­лучим условия максимума и минимума интерференции для раз­ности фаз δ _max = ±2πm и δ _min = ±(2m+1)π, ( m = 0,1,2…).

Если амплитудные значения светового вектора не равны друг другу, т.е. Е₀₁ ≠ Е₀₂, то квадрат результирующей амплитуды определяется по формуле:

Е² = Е₀₁² + Е₀₂² + 2Е₀₁Е₀₂cos (φ₂ – φ₁),

где (φ₂ – φ₁) – разность фаз колебаний. Поскольку интенсив­ность света I пропорциональна квадрату амплитудного значения Е, то

.

В точках пространства, где cos (φ₂ – φ₁) > 0, результирующая интенсивность I > I₁ + I₂. Если cos (φ₂ – φ₁) < 0, то I < I₁ + I₂. Та­ким образом, мы наблюдаем перераспределение интенсивности и интерференционную картину.