Теорема о кинетической энергии: приращение кинетической энергии тела равно алгебраической сумме работ, совершаемых всеми действующими на него силами, т.Е.:

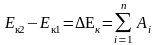(4.8)

Т.о., кинетическая энергия является функцией массы и скорости тела; всегда неотрицательная величина; характеризует способность тела совершать работу, т.е. обмениваться механическим движением с другими телами.

В общем случае работа силы является функцией процесса, т.е., ее величина зависит от того, каким путем тело переходит из начального положения в конечное. Однако в природе существует ряд сил, работа которых не зависит от формы траектории движения тела, а определяется лишь его начальным и конечным положениями. Такие силы называются потенциальными или консервативными. Для них вводится понятие потенциальной энергии Е_п.

Потенциальная энергия – это СФВ, являющаяся мерой взаимодействия тел или частей одного и того же тела и определяемая их взаимным расположением и характером сил взаимодействия между ними.

В отличие от кинетической, потенциальная энергия может быть как положительной, так и отрицательной, т.е., нулевой уровень потенциальной энергии можно задавать произвольно, исходя из условий данной задачи. Работу потенциальных сил записывают так

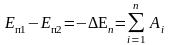. (4.9)

Уравнение (4.9) – математическая форма записи теоремы о потенциальной энергии: работа консервативных сил, действующих на данное тело (или его части) при изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус (знак «минус» означает, что работа совершается за счет убыли потенциальной энергии).

При элементарном (бесконечно малом) изменении конфигурации системы работа консервативных сил равна:

dA = -dE_п (4.10)

или, с учетом (4.1)

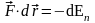_(4.11)

Потенциальная энергия равна

, (4.12)

где С – постоянная интегрирования. Т.о., потенциальная энергия определяется с точностью до некоторой произвольной постоянной, которая зависит от выбора нулевого уровня отсчета.

Для консервативных сил можно записать:

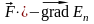, (4.13)

где

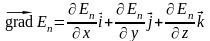, (4.14)

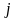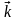( , _, - единичные векторы координатных осей). Вектор, определяемый выражением (4.14), называется градиентом скаляра Е_п.

Конкретный вид формулы для потенциальной энергии зависит от характера силового поля, т.е., от того, какие силы действуют в системе. Примеры потенциальных энергий:

а) Потенциальная энергия упругодеформированного тела (пружины):

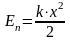, (4.15)

где k - коэффициент упругости (жесткость пружины), х - абсолютная деформация тела (пружины).

б) Потенциальная энергия гравитационного взаимодействия двух тел

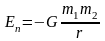, (4.16)

где m₁ и m₂ – массы тел, G = 6.6710^-11 Нм²/кг² – гравитационная постоянная, г– расстояние между центрами масс взаимодействующих тел.

в) Потенциальная энергия тела массы m, находящегося в однородном поле силы тяжести (поднятого над поверхностью планеты):

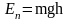, (4.17)

где h – высота тела над уровнем, принятым за нулевой и h много меньше радиуса планеты, g - ускорение свободного падения на планете.

Механической энергией Е тела называется сумма его кинетической и потенциальной энергий

Е = Т + П = Const (4.18)

Полной механической энергией системы тел называется сумма механических энергий тел, входящих в состав данной системы

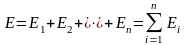(4.19)

Система тел называется изолированной (замкнутой), если на нее не действуют никакие внешние силы.

Для замкнутой системы тел выполняются фундаментальные законы механики – законы сохранения.