- •Н.И.Ильиных, в.Е.Сидоров, л.С.Кандазали физика
- •Часть 1. Механика. Молекулярная физика и термодинамика.
- •230105.65 «Программное обеспечение вычислительной техники и автоматизированных систем»,
- •230100.62 «Информатика и вычислительная техника (бакалавр техники и технологии)» Екатеринбург
- •Рецензент: доцент кафедры общей физики и естествознания УрГпу, к.Ф.-м.Н Сабирзянов а.А.
- •Содержание
- •Пояснительная записка
- •Перечень практических работ
- •Общие методические указания к решению задач
- •Практическое занятие 1
- •Средняя скорость в течение конечного промежутка времени t при равномерном прямолинейном движении в направлении оси движения х равна
- •Ускорение при равнопеременном прямолинейном движении в направлении оси движения х равно:
- •Примеры решения задач.
- •Задачи для самостоятельного решения.
- •Практическое занятие 2
- •Примеры решения задач.
- •Задачи для самостоятельного решения.
- •Практическое занятие 3
- •Теорема о кинетической энергии: приращение кинетической энергии тела равно алгебраической сумме работ, совершаемых всеми действующими на него силами, т.Е.:
- •Закон сохранения импульса.
- •Закон сохранения энергии.
- •Примеры решения задач.
- •Задачи для самостоятельного решения.
- •Практическое занятие 4
- •Примеры решения задач
- •Задачи для самостоятельного решения.
- •Практическое занятие 5
- •Примеры решения задач.
- •Задачи для самостоятельного решения.
- •Список литературы
- •Приложение 2
- •Приложение 5
- •Приложение 6
Средняя скорость в течение конечного промежутка времени t при равномерном прямолинейном движении в направлении оси движения х равна
 (1.1)
(1.1)
Мгновенная
скорость
при t
0 равна:
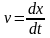 .
.
Прямолинейное равномерное движение с постоянной скоростью вдоль оси х при t0 = 0 описывается уравнением
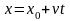 (1.2)
(1.2)
где х0 - начальная координата движущейся точки.
Ускорение при равнопеременном прямолинейном движении в направлении оси движения х равно:
 (1.3)
(1.3)
Мгновенное ускорение при t 0 равно:
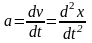 . (1.4)
. (1.4)
Уравнение
прямолинейного равнопеременного
движения с начальной скоростью
 вдоль оси х
имеет
вид:
вдоль оси х
имеет
вид:
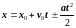 , (1.5)
, (1.5)
где знак “ – “ берется для равнозамедленного движения.
Путь при прямолинейном равнопеременном движении равен модулю перемещения:
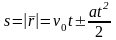 (1.6)
(1.6)
При равнопеременном движении уравнение скорости вдоль оси х принимает вид:
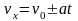 (1.7)
(1.7)
Для равнопеременного движения справедливо равенство, не содержащее времени:
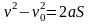 (1.9)
(1.9)
В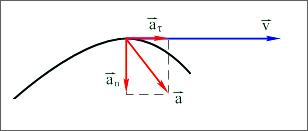 случае криволинейного движения
направление вектора ускорения не
совпадает с направлением вектора
скорости Составляющие вектора ускорения
называют касательным (тангенциальным)
и нормальным( центростремительным)
ускорениями (см. рис.1.1.).
случае криволинейного движения
направление вектора ускорения не
совпадает с направлением вектора
скорости Составляющие вектора ускорения
называют касательным (тангенциальным)
и нормальным( центростремительным)
ускорениями (см. рис.1.1.).
К
Рис. 1.1.
асательное ускорение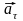 характеризует быстроту изменения
скорости по модулю:
характеризует быстроту изменения
скорости по модулю:
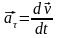 (1.10)
(1.10)
Вектор направлен по касательной к траектории.
Нормальное
ускорение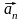 характеризует быстроту изменения
скорости по направлению и направлено
всегда к центру кривизны траектории.
Нормальное ускорение зависит от модуля
скорости υ и от радиуса R окружности, по
дуге которой тело движется в данный
момент времени:
характеризует быстроту изменения
скорости по направлению и направлено
всегда к центру кривизны траектории.
Нормальное ускорение зависит от модуля
скорости υ и от радиуса R окружности, по
дуге которой тело движется в данный
момент времени:
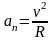 (1.11)
(1.11)
Примеры решения задач.
Задача
1. Зависимость
координаты тела от времени имеет
следующий вид:
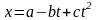 ,
где
,
где
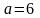 м,
м,
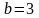 м/с,
м/с, м/с
м/с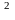 .
Найти среднюю скорость <v>
и среднее ускорение <a>
в интервале времени от 1 до 4 с.
.
Найти среднюю скорость <v>
и среднее ускорение <a>
в интервале времени от 1 до 4 с.
Дано:
м м/с м/с t1 = 1c t2 = 4c |
Решение:
По
определению, средняя скорость
Находим численное значение средней скорости:
|
<v> - ?
|
|
|
По
определению
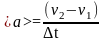 ,
где v1
и v2
мгновенные скорости при t1
и t2,
соответственно. Мгновенную скорость
найдем как
,
где v1
и v2
мгновенные скорости при t1
и t2,
соответственно. Мгновенную скорость
найдем как
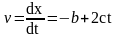 .
Среднее
ускорение равно:
.
Среднее
ускорение равно:
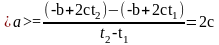
Численное
значение среднего ускорения:
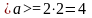 (м/с
).
(м/с
).
Ответ: <v> = 7 м/с, <a> = 4 м/с2.
Задача
2. Радиус-вектор
частицы меняется со временем
 по закону
по закону
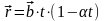 ,
где
,
где
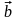 – постоянный вектор,
– постоянный вектор,
 – положительная постоянная. Найти: а)
скорость
и ускорение
– положительная постоянная. Найти: а)
скорость
и ускорение
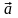 частицы
в зависимости от времени;
частицы
в зависимости от времени;
б) промежуток времени t, по истечении которого частица вернётся в исходную точку;
в) путь S, который она пройдёт при этом.
Дано:
______________ |
Решение. Найдём скорость и ускорение частицы по формулам:
Для определения интервала времени t учтём, что при t = t . |
(t) - ? t - ? S - ? |
|
На
рис.1.1 изображена зависимость
радиус-вектора
Тогда
О |
|
Задача 3. При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определить перемещение тела за cедьмую секунду.
Дано:
|
СИ: 0,9м |
Решение. Проведем
ось
|
|
|
|
По условию задачи x0 = 0, v0 = 0. Следовательно:
Перемещение
тела за пятую секунду равно:
Следовательно:
Подставим численные значения, произведем вычисления:
Ответ: |
||
Задача 4. С башни высотой Н = 25 м горизонтально брошен камень со скоростью υ0 = 15 м/с. Определить: 1) уравнение траектории y=y(x)$ 2) время движения камня; 3) на каком расстоянии Sх от основания башни он упадет на землю; 4) с какой скоростью υ он упадет на землю; 5) какой угол φ составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать.
Дано: Н = 25 м υ0 = 15 м/с |
Р
где
|
1) y(x) = ? 2) t = ? 3) sх = ? 4) υ = ? 5) φ = ? |
|
|
|
Так как при данном выборе системы отсчета x0 =0, ax = 0, v0x = v0, y0 = H, v0y =0, ay = g, то эти уравнения запишутся следующим образом:
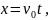
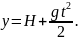
Т.о., видно, что движение по оси х равномерное, по оси y - равноускоренное.
Выразим время t из уравнения для х и подставим в уравнение для у, получаем:
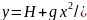 ).
).
Подставим численные значения, получаем уравнение траектории:
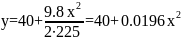 .
.
2) Найдем общее время движения (временя полёта). Так как координата у в момент падения равна 0 (y = 0), можно записать:
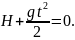
Решаем это уравнение относительно t, получаем:
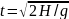 .
.
Подставляем численные значения, получаем:
t
=
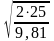 ≈ 2,26 (c).
≈ 2,26 (c).
3) Для нахождения дальности полёта воспользуемся формулой равномерного движения. Перемещение вдоль оси x равно:
Sх = υ0хt = υ0t.
Подставляем численные значения, получаем:
Sх = 152.26 = 33.934 м.
4)
Для нахождения скорости
приземления
разложим вектор скорости на два вектора
 и
и
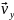 так, чтобы
так, чтобы
 (см. рисунок) и рассмотрим треугольник
векторов скоростей. По теореме Пифагора:
(см. рисунок) и рассмотрим треугольник
векторов скоростей. По теореме Пифагора:
υ
=
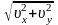 .
.
Скорость по оси x не изменяется:
vx = v0x +axt= v0.
Скорость по оси y равна:
vy = v0y +ayt= gt
Тогда полная скорость приземления:
υ
=
 =
=
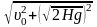 =
=
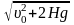
υ
=
 ≈ 26,749 (м/с).
≈ 26,749 (м/с).
5) Из треугольника скоростей в точке приземления: υх = υ0 = υсosφ,
Тогда угол приземления камня:
φ
= arccos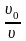 = arccos
= arccos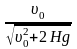
φ
= arccos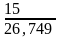 = arccos0,56077 ≈ 55,891º ≈ 56º.
= arccos0,56077 ≈ 55,891º ≈ 56º.
Ответ: t = 2,26 с, Sx = 33,9 м, υy = 22,1 м/с, υ = 26,7 м/с, φ = 56°

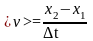 ,
где x1
и x2
- координаты
тела в моменты времени t1
и t2,
t
= t2
- t1.
Для средней
скорости получаем:
,
где x1
и x2
- координаты
тела в моменты времени t1
и t2,
t
= t2
- t1.
Для средней
скорости получаем: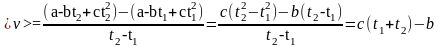 .
.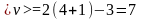 (м/с).
(м/с).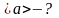
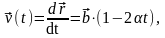
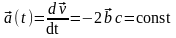 .
. ?
?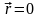 .
Следовательно,
.
Следовательно,
 ,
,
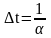
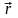 от времени, из которой следует, что
от времени, из которой следует, что
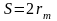 (т.к. движение прямолинейное) и
(т.к. движение прямолинейное) и
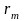 определяется соотношением:
определяется соотношением:
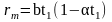 ,
где
,
где
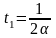 .
.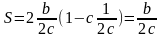
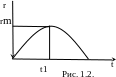 твет:
твет:
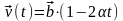 ;
;
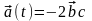 ;
;
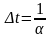 ;
S
= b/2c
;
S
= b/2c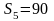 см
см в направлении движения тела, а начало
координат совместим с точкой, из
которой тело начинает движение. Запишем
уравнение движения:
в направлении движения тела, а начало
координат совместим с точкой, из
которой тело начинает движение. Запишем
уравнение движения: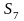 -
?
-
?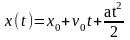 .
.
 ;
;
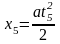 ,
где
,
где
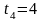 с,
с,
 с.
с.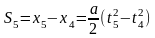 ,
откуда
,
откуда
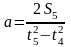 .
Аналогично, перемещение тела за седьмую
секунду:
.
Аналогично, перемещение тела за седьмую
секунду:
 ,
где
,
где
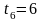 с,
с,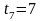 с.
с.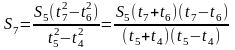 .
.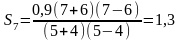 (м).
(м). 1,3
м.
1,3
м.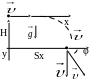 ешение.
ешение.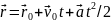 ,
,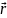 радиус – вектор в произвольный момент
времени t,
радиус – вектор в произвольный момент
времени t,
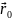 - радиус – вектор в начальный момент
времени,
- радиус – вектор в начальный момент
времени,
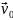 – начальная скорость,
– начальная скорость,
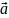 – ускорение. Выберем систему координат
(см. рисунок) и запишем проекции этого
уравнения на оси х
и у:
– ускорение. Выберем систему координат
(см. рисунок) и запишем проекции этого
уравнения на оси х
и у: