7)Неперервність функції в точці та на проміжку. Властивості неперервних функцій.

Функцію називають неперервною в точці , якщо вона визначена в цій точці і в деякому її околі і , тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції. Якщо функція неперервна в кожній точці проміжку , то вона називається неперервною на цьому проміжку.

Властивості

Якщо функція неперервна в кожній точці інтервалу (а,b), то вона називається

неперервною на цьому інтервалі.

Функція неперервна на відрізку [а,b], якщо вона неперервна на (а,b) і, крім того,

неперервна справа в точці а і зліва в точці b.

Сформулюємо теореми про неперервні функції.

Теорема 1 (перша теорема Больцано-Коші). Якщо функція y = f (x)

неперервна на відрізку [а; b] і на його кінцях набирає значень різних знаків, то

всередині відрізка [а; b] знайдеться хоча б одна точка x = c , в якій функція

дорівнює нулю.

Теорема 2 (друга теорема Больцано-Коші). Нехай функція y = f (x)

неперервна на відрізку [а; b] і набуває на його кінцях різних значень: f (a) =/ f (b) .

Тоді для довільного числа и є [ f (a); f (b)] знайдеться таке число c(a; b) , що

f (c) є и .

Теорема 3 (Вейєрштрасса). Якщо функція y  f (x) неперервна на відрізку

[а; b], то серед її значень на цьому відрізку існує найбільше і найменше.

8) Якщо хоча б одна з умов неперервності функції в точці не виконується, то

функція розривна в точці x0 , а саму точку x0 називають точкою розриву функції.

Класифікація точок розриву проводиться таким чином:

1. якщо існують лівостороння і правостороння границі функції в точці , тобто ,

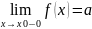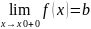, де a і b –скінченні числа, причому а не дорівнює b, то точку x0 називають точкою розриву першого роду; відмітимо, що в точці

x0 сама функція може бути як визначена так і невизначена;

2) якщо хоча б одна з границь 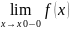, не існує або дорівнює

нескінченості, то точку x0 називають точкою розриву другого роду, в точці x0

функція робить “нескінченний стрибок”

3) якщо 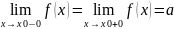, , 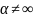f(x0)≠a або в цій точці функція

невизначена, то точку x0 називають усувною точкою розриву

9) Похідною функції y = f(x) у точці Х називають число, до якого прямує відношення 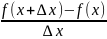Похідну функції f(x) позначають f'(x).

Фізичний зміст похідної. Якщо матеріальна точка рухається прямолінійно і її координата змінюється за законом S = S(t), то швидкість її руху v(t) у момент t дорівнює похідній S'(t): v(t) = S'(t)

Геометричний зміст похідної: значення похідної функції y = f(x) у точці x₀ дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x₀: y' = f'(x₀) = k = tgα.

Зв’язок між неперервністю і диференційовністю функції встановлює теорема.

Теорема. Якщо функція диференційовна в деякій точці, то у цій точці функція неперервна.

10) Основні правила диференціювання.

Теорема 1. Похідна сталої дорівнює нулю.

y = c, то y΄ = 0

Теорема 2. Похідна алгебраїчної суми скінченого числа диференційованих функцій дорівнює алгебраїчній сумі похідних цих функцій

Теорема 3 Похідна добутку двох диференційованих функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:

Теорема 4 Сталий множник виносимо за знак похідної

 

(cu)΄ = cu΄, де c = const

Теорема 5 Якщо чисельник і знаменник дробу диференційовані функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різниця добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат знаменника початкового дробу

₁₁ ; ; ; ; ;

; ; ; ; ; ; ; ; ; ; ; ; .
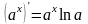
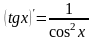
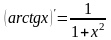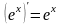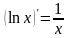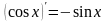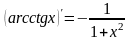