19(21). Спектральная плотность постоянного во времени сигнала.
Простейший
неинтегрируемый сигнал это постоянная
во времени величина
.
Предположим,
что
-
произвольный, вещественный и абсолютно
интегрируемый сигнал. В соответствие
ему поставим спектральную плотность
.
Воспользовавшись последним равенством
можно записать.
(7)
Равенство
(7) выполняется только в том случае, если
спектральная плотность
.
Физический смысл последнего равенства нагляден: постоянный во времени сигнал имеет спектральную составляющую в виде дельта функции на нулевой частоте.
20. Обобщенная формула Рэлея.
В дальнейшем нам понадобятся следующие вспомогательные результаты. Пусть два сигнала U(t) и V(t) связанны следующими преобразованиями.
(1)
(2)
22. Спектральная плотность неинтегрируемых сигналов.
Спектральная плотность -функции.
П
усть
сигал
представляет собой короткий импульс,
сосредоточенный в точке и имеющий
единичную площадь. Такой сигнал имеет
математическую модель.
Спектральная плотность:
23.Спектральная плотность сигнала, смещенного во времени.
Пусть
сигнал
существует на интервале от
до
.И
ему в соответствие поставлена спектральная
плотность
.
При
задержке сигнала
на время
получим новую функцию от времени. Новая
функция существует в интервале времени
от
до
,
.
25. Спектральний аналіз неперіодичних сигналів. Умови існування спектральної щільності сигналу.
1.Пусть одиночный сигнал задан некоторой функцией, отличной от 0 на интервале времени от t1 до t2. Выделим произвольный интервал времени от t1 до t2 ,который является подмножеством интервала T и мысленно расположим в каждом интервале T эквивалентные импульсы. Можно считать данный сигнал периодическим, а значит он может быть разложен в ряд Фурье.
(1)
где
Коэффициенты данного ряда определяются из выражения.
(2)
28 Спектральний аналіз періодичних сигналів.
Періодичним
називається будь-який сигнал, для якого
виконується умова:
T- період.
Будь-який
періодичний сигнал можна представити
у виді суми елементарних складових
(базисних функцій). Якщо базисною функцією
є гармонійний сигнал то ряд Фур'є має
вид:
Спектр ф-ції – графічне представлення ряду Фур’є.
Прямокутні сигнали мають спектр у вигляді арочного синуса. При цьому виникає залежність: q=T/ti
30-31. Модульовані сигнали. Амплітудна модуляція. Спектр однотональних АМ коливань.
В
самом общем случае модулирующий сигнал
можно представить в виде
(1)
В
формуле (1)
и
изменяются
по закону информационного сигнала.
Если
,
то выражение (1) превращается в простой
ВЧ гармонический сигнал. В этом случае
он ни какой информации не несет. В
зависимости от того какой из параметров
ВЧ колебания изменяется,
или
различают два вида модуляций - амплитудную
модуляци
и угловую
модуляцию.
Угловая в
свою очередь на основе природы изменения
угла косинуса несущего колебания делится
на фазовую и частотную. Закон изменения
параметров
и
настолько медленно меняются, что их
можно назвать низкочастотными или
медленноменяющимися.
1.Амплитудная модуляция Однотональная.
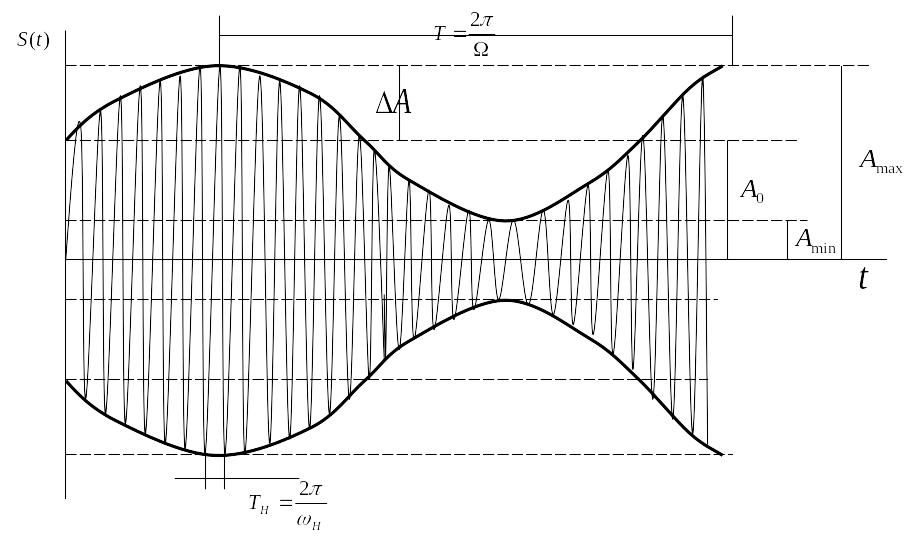
При АМ амплитуда несущего колебания является функцией времени и имеет вид.
где
-постоянная
составляющая ( среднее значение амплитуды
модулируемого колебания),
-функция
времени, которая называется модулирующей
функцией.Для одно-тональной модуляции
формула АМ колебания записывается.
Коэффициент
модуляции изменяется в пределах от нуля
до единицы. Или в относительных единицах
от нуля до 100%.
где
-глубина
модуляции.Если
-наблюдаем
перемодуляцию.
В режиме перемодуляции происходит искажение сигнала информации
Спектр однотональных АМ колебаний.
На основе тригонометрических преобразований разложим АМ колебание на сумму элементарных функций.
-
частота нижней боковой составляющей.
-
частота верхней боковой составляющей.
-
фаза нижней боковой составляющей.
-
фаза верхней боковой составляющей.