1. Периодические сигналы и ряды Фурье.

Периодическим сигналом называется любой сигнал, для которого выполняется условие , где n=1,2,3…, Т- период следования сигналов.

t

Любой периодический сигнал можно представить в виде суммы элементарных составляющих (базисных функций). Если базисной функцией является гармонический сигнал то ряд Фурье имеет вид: (28.1)

-круговая частота, определяемая величиной периода.

Введем основные формулы ряда Фурье: зададим на отрезке времени ортонормированный базис, образованный гармоническими функциями с кратными частотами: ; ; ; ; и т.д. (28.2)

На основании принятой Фурье за базисные функции набора ортонормированных гармонических функций можно вывести формулы для нахождения коэффициентов и параметров ряда Фурье.

-постоянная составляющая ряда Фурье.

- косинусная составляющая ряда Фурье.

-синусная составляющая ряда Фурье.

Запишем вторую тригонометрическую форму записи ряда Фурье:

(28.3)

2. Амплитудно-частотный спектр

Огибающая АЧС последовательности прямоугольных видеоим­пульсов описывается функцией

.

Рассмотрим комплексный спектр периодической последовательности прямоугольных видео импульсов.

и пересекает ось частот, когда х кратно л, т. е. п кратно q, τ. е. при частотах, кратных скважности. Поэтому именно эти частоты, равные

отсутствуют в спектре.

3. СПЕКТРЫ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

Прямоугольных видеоимпульсов

Пусть w(t) определяет периодическую последовательность пря­моугольных видеоимпульсов с амплитудой U_m, длительностью t_И и периодом следования (рис. 15.4).

Функция u(t) в пределах периода может быть описана как

4. Спектральний аналіз періодичної послідовності відео імпульсів (t₀=0).

6. Спектральный анализ периодической последовательности радио импульсов.

(єквивалентно ) -несущая частота.

Аналитическая форма записи.

(28.11)

7. Спектральний аналіз неперіодичних сигналів. Неперіодичний прямокутний відео імпульс.

Пусть одиночный сигнал задан некоторой функцией, отличной от 0 на интервале времени от t₁ до t₂. Выделим произвольный интервал времени от t₁ до t₂ ,который является подмножеством интервала T и мысленно расположим в каждом интервале T эквивалентные импульсы. Можно считать данный сигнал периодическим, а значит он может быть разложен в ряд Фурье.

(1)

где

Коэффициенты данного ряда определяются из выражения.

(2)

8. Спектральная плотность аналоговых сигналов.

Пара преобразований Фурье.

В связи с тем, что спектр становится сплошным вводится поня­тие спектральной плотности, которая является мерой количества энергии на единицу частоты.

На основе данных рассуждений дискретная частота не будет изменяться дискретно, а за­меняется на непрерывную частоту , а .

После соответствующих преобразований перейдем к двойному интегралу Фурье.

(4)

Внутренний интеграл в выражении (4) является функцией частоты. Это и есть спектральная плотность.

(5)

9.Свойство вещественной и мнимой части спектральной плотности.

Пусть -сигнал, принимающий вещественные значения. Его спектральная плотность в общем случае является комплексной величиной, а следовательно может быть представлена в виде.

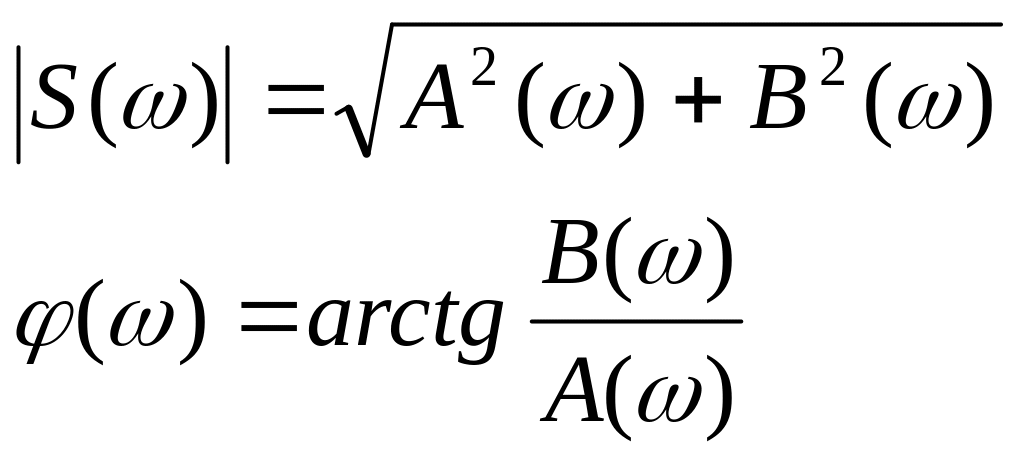
Величины и представляют собой соответственно вещественную и мнимую части спектральной плотности. и -модуль и аргумент спектральной плотности.

(9)

10. Зависимость спектральной плотности сигнала от выбора масштаба измерения времени.

Пусть сигнал с заданной внутренней структурой подвергается во временной области сжатию в -раз. При этом форма и амплитуда сигнала сохранены.

Новый сигнал связан с исходным соотношением , где . Длительность сигнала в -раз меньше сигнала . Спектральная плотность сжатого сигнала равна:

(12)

(12*)

Интеграл в правой части (5) представляет собой спектральную плотность исходного сигнала при частоте , т.е. .