20. Допускаемое напряжение, и факторы влияющие на его величину

Напряжение в поперечных сечениях стержня

Нормальная сила   приложена в центре тяжести сечения, яв­ляется равнодействующей внутренних сил в сечении и, в соответст­вии с этим, определяется следующим образом:

.

Но из этой формулы нельзя найти закон распределения нор­мальных   напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямо­угольную сетку (рис. 2.2, б), то после нагружения поперечные ли­нии аа, bb и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что по­перечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений (гипотезе Бернулли).

Значит, все продольные волокна стержня находятся в одина­ковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и рав­ны

,                                                                                                                          (2.2)

где A  площадь поперечного сечения стержня.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 2.7, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения  , одинаковы:   (рис. 2.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 2.7, в).          

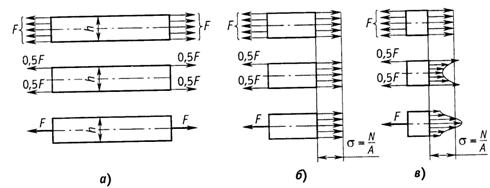
Рис.2.7

 

Высказанное предположение о равномерном распределении нормальных напряжений в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения пло­щади поперечного сечения (рис. 2.2, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций.

Нормальные напряжения при сжатии определяют также, как и при растяжении, но считают отрицательными.

Следует помнить, что длинные (тонкие) стержни, нагруженные сжимающими силами, могут потерять устойчивость. Расчет стержней на устойчивость рассмотрен в разделе «Устойчивость». 

В инженерных сооружениях встречаются растянутые или сжатые элементы, имеющие отверстия. В сечениях с отверстием определяют осредненные нормальные напряжения по формуле

,                                                                                                                        (2.3)

где    площадь поперечного сечения нетто;  - площадь поперечного сечения брутто;  - площадь его ослабления.

21. Статически неопределимые задачи при растяжении. Учет изменения температуры

Системы, в которых неизвестные могут быть определены с помощью

одних  уравнений  статики,  называются  статически  определимыми (СОС). Чтобы система была статически определимой, число неизвестных не должно превышать числа уравнений, составляемых по правилам статики. Если число неизвестных больше возможного числа уравнений равновесия статики, система становится статически неопределимой (СНОС).

Для решения статически неопределимых систем необходимо в дополнение к уравнениям статики составить уравнения перемещений. Число уравнений перемещений должно соответствовать числу неиз- вестных системы.

Число неизвестных определяет степень статической неопределимости системы. Если система имеет одно, два и т. д. неизвестных, то ее назы- вают один раз (или однажды), два раза (или трижды) и т. д. статически неопределимой. Число уравнений перемещений должно соответствовать степени  статической  неопределимости.  Наиболее  трудной  частью решения статически неопределимых систем является составление уравнений перемещений, которые отображают большое разнообразие физических  явлений,  происходящих  в  системе.  Следует  отметить,  что если в статически определимых системах усилия в упругих элементах могут возникать только от активных и реактивных внешних сил, то в статически неопределимых системах усилия могут возникать и от других причин, например, от изменения температуры, неточностей изготовления элементов системы. Во второй части методического пособия приводятся ряд примеров правила составления уравнений перемещений и методы решения статически неопределимых систем.

22. Учет неточности изготовления в статически неопределимых задачах

Наличие в таблице отдельных значений ампервитков срабатывания для улучшенной стали также не может быть оправдано, ибо влияние проницаемости стали на ампервитки срабатывания значительно меньше, чемвлияние неточности изготовления деталей, сборки и регулировки реле. [1]

Значение усилий в статически неопределимых конструкциях зависит в случае силовых внешних воздействий от соотношения между поперечными размерами на отдельных участках конструкции, а в случае температурного воздействия или влияния неточности изготовления деталей - от абсолютных значений этих размеров. Поэтому при решении статически неопределимых задач приходится задавать размеры поперечных сечений для отдельных частей конструкции или же принимать определенное соотношение между этими размерами. [2]

Если статически неопределимая система подвергается только изменению температуры, то свободными членами канонических уравнений будут б /, представляющие собой обобщенные перемещения, соответствующие / - той лишней неизвестной обобщенной силе в основной системе от изменения температуры. Учет влияния неточности изготовления элементов системы при ее монтаже производят введением в свободные члены канонических уравнений величины б - д, выражающей обобщенные перемещения, соответствующие / - той лишней неизвестной обобщенной силе в основной системе от неточности Л изготовления элементов. [3]

Если статически неопределимая система подвергается только изменению температуры, то свободными членами канонических уравнений будут 6Л, представляющие собой обобщенные перемещения, соответствующие i - й лишней неизвестной обобщенной силе в основной системе от изменения температуры. Учет влияния неточности изготовления элементов системы при ее монтаже производят введением в свободные члены канонических уравнений величины 8 д, выражающей обобщенные перемещения, соответствующие i - й лишней неизвестной обобщенной силе в основной системе от неточности А изготовления элементов. [4]

Как показано в § 4 - 10, величины Q2H и 6Q определяют при испытаниях опытным путем. Для этого значения 5 и / п следует находить непосредственным измерением во избежание влияния неточностей изготовления деталей насоса на результаты его испытаний. [5]

К расчету.

Из этой формулы видно, что точность изготовления рефлектора в центральной части должна быть большей, чем по краям рефлектора. К тому же края рефлектора возбуждаются менее интенсивно, что приводит к уменьшению влияния неточности изготовления краев рефлектора а диаграмму направленности антенны. [6]

В этих случаях обязат зльны осевая фиксация и крепление колес на валах. Неравномерн) сть распределения нагрузки в шпоночном и шлицевом соед гниях усиливается, их несущая способность понижается при увели1 ении 1Ст из-за возрастающего влияния неточностей изготовления и; гла закручивания. [7]

Таким образом, для рассмотренного типа поршневого насоса силы трения в механизмах привода и уплотнении поршня могут быть относительно боагьшими. Это существенно ухудшает эксплуатационные свойства насосов, например, экономичность или срок слухбн, и требует повысить точность изготовления ж использовать конструктивные решения, уменьшающие влияние неточности изготовления на рабочий процесс. [8]

Давление воздуха между входным соплом и имеющимся зазором в неплотностях цилиндропоршневой группы двигателя измеряется манометром 6, шкала которого проградуирована в процентах утечки: чем больше неплотность в цилиндропоршневой группе, тем больший процент утечки покажет манометр. Измерения проводят в начале и конце такта сжатия. Для устранения влияния неточности изготовления входного сопла на градуировку шкалы имеется регулировочный винт 8, который регулируется на заводе. [9]

Они обусловлены: отклонением закона распределения индукции в воздушном зазоре от синусоидального и неточностью изготовления сельсинов. Несинусоидальность распределения индукции снижается конструктивно, а влияние неточности изготовления и неравенства параметров фаз обмоток синхронизации могут быть уменьшены включением в цепи синхронизации резисторов, индуктивных катушек и конденсаторов, параметры которых подбираются экспериментально. [10

23-25. Инженерные методы расчета на прочность. Метод допускаемых напряжений

При проектировании различных инженерных сооружений и машин приходится определять размеры отдельных элементов этих сооружений и деталей машин. Эти задачи решаются на основании расчетов, целью которых является создание прочных, устойчивых, долговечных и экономичных сооружений. Все эти вопросы рассматриваются в комплексе дисциплин, основой которых является “Сопротивление материалов”.

    При нагружении отдельного элемента сооружения внешней нагрузкой в нем возникают внутренние силы (продольные и поперечные силы, изгибающие и крутящие моменты). Интенсивность внутренних сил называется напряжением (нормальное –   и касательное –  ).

    Чтобы судить о прочности элемента, необходимо провести специальные расчеты. Существует три метода таких расчетов:

    – расчет по допускаемым напряжениям;

    – расчет по разрушающим нагрузкам;

    – расчет по предельным состояниям.

    Остановимся подробно на расчете по допускаемым напряжениям.

    Условие прочности по допускаемым напряжениям имеет вид:

 или  ,

где   – максимальные напряжения в опасном поперечном сечении стержня;   – допускаемые напряжения.

   ,

где   – предел текучести материала; К – коэффициент запаса прочности.

    На основании условия прочности стержня можно решить три типа задач:

• проверить прочность стержня;

• найти необходимые размеры поперечного сечения стержня;

• установить допускаемую грузоподъемность.

    Кроме расчета на прочность, отдельный элемент проверяется еще и на жесткость. Проверка стержня на жесткость состоит в определении его деформации и сравнении ее с допускаемой величиной.