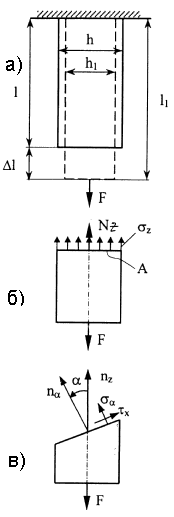
Центральное (осевое) растяжение-сжатие

Осевым растяжением (сжатием) брусьев называют такой вид деформирования, при котором в их поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N_z. Для определения продольной силы используется метод сечений (Рис. 4.1,б).

N_z= Σ F_z^вн      (4.1)

Напряжения

N_z равномерно распределяется по площади поперечного сечения, вызывая нормальные напряжения.

В наклонном сечении возникают нормальные  σ_α и касательные  τ_α напряжения (рис. 4.1,в).

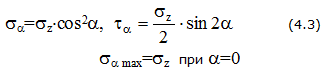
               причем

Деформации

При растяжении (сжатии) наблюдаются абсолютные и относительные деформации (рис. 4.1,а):

l₁ – l =  Δl - абсолютная продольная деформация (удлинение);

h₁ – h = -Δh - абсолютная поперечная деформация (сужение);

относительная продольная деформация:

относительная поперечная деформация:

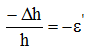
Отношение

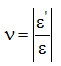
называется коэффициентом поперечной деформации (коэффициентом Пуассона).

Напряжения и деформации взаимосвязаны законом Гука 

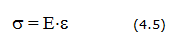
где Е - модуль упругости (модуль Юнга).     

В общем случае удлинение стержня определяется по формуле

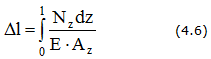
В частном случае, когда жесткость сечения  ЕА = const  и N_Z = F = const

При ступенчатом изменении нагрузки N_z и конфигурации сечения

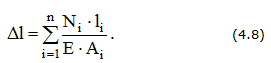
В результате деформации бруса его поперечные сечения получают линейные перемещения U_(z). Так, перемещение сечения В, находящегося на расстоянии z от закрепленного конца, равно удлинению Δl_z части бруса длиной z, заключенной между неподвижным и рассматриваемым сечением.

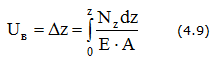Взаимное перемещение двух сечений В и С бруса равно удлинению части бруса, заключенной между этими сечениями  

  

        U_(B-C)=  Δl_B-C             (рис.4.2)

Рис. 4.2

Перемещение точек стержневой системы (BCD)  (Рис. 4.3) происходит как за счет продольных деформаций (U_СВ =   Δl_BC , U_CD =   Δl_DC ), так и за счет поворота деформированных стержней  BC₁ и DC₂ относительно шарниров (B, D) как твердого тела по дугам  С₁С₃ =  δ₁ и С₂С₃ =  δ₂, замененными перпендикулярами к радиусам поворота (ВС₁ и DС₂). Отрезок СС₃ =  δ_с соответствует полному перемещению узла С в результате деформации стержней ВС и DС.

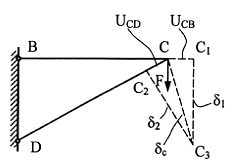
Рис. 4.3

Условие прочности при растяжении сжатии

Условие прочности при растяжении (сжатии) выражается неравенством:

где [σ] – допускаемые напряжения, определяются как:

n – коэффициент запаса прочности, устанавливаемый нормативными документами.

Условие прочности позволяет решать три типа задач:

1. Проверка прочности (проверочный расчет)

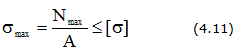
2. Подбор сечения (проектировочный расчет)

3. Определение грузоподъемности (допускаемой нагрузки) 

Условие жесткости

Условие жесткости стержня

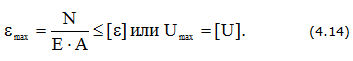
Условие жесткости узла стержневой системы

Потенциальная энергия упругой деформации стержня 

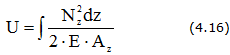
12. Напряжения и перемещения поперечных сечений прямоугольного бруса от переменной осевой нагрузки..

13.Расчетная схема.

14. Потенциальная энергия упругой деформации при растяжении прямого бруса

А=U+K. (В результате работы накапливается потенциальная энергия деформированного тела U, кроме того, работа идёт на совершение скорости массе тела, т.е. преобразуется в кинетическую энергию). Если центральное растяжение (сжатие) бруса из линейно-упругого материала производится очень медленно, то скорость перемещения центра масс тела будет весьма малой. Такой процесс нагружения называется статическим. Тело в любой момент находится в состоянии равновесия. В этом случае А=U, и работа внешних сил целиком преобразуется в потенциальную энергию деформации.  ,  ,  .