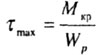8. Внутренние силы и метод их определения. Простые деформации

Под действием внешних сил на объект, происходит изменение между частицами (атомами) рассматриваемого тела и сил взаимодействия между ними. В результате возникают внутренние усилия, которые определяются методом сечения РОЗУ

Для определения внутренних усилий методом сечений необходимо:

А) Рассечь конструкцию произвольным сечением ( отбрасывается одна из частей)

Заменяется отброшенная часть внутренними усилиями, составляются уравнения для нахождения внутреннего усилия.

Простые деформации

• растяжение-сжатие,

• сдвиг,

• изгиб,

• кручение.

9.Дифференциальные зависимости между q, q, m при изгибе Дифференциальные зависимости при изгибе

Вы делим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dz. Так как вся балка находится в равновесии, то и элемент dz будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Q_y и M_x в об щем случае меняются вдоль оси балки, то в сечениях элемента dz будут возникать поперечные силы Q_y иQ_y+ dQ_y, а также изгибающие моменты M_x и M_x+dM_x.  Из условия равновесия выделенного элемента получим: , следовательно  ; (6.5) , следовательно  (6.6) Первое из двух записанных уравнений дает условие  (6.7) Из второго уравнения, пренебрегая слагаемым   как бесконечно малой величиной второго порядка, найдем  (6.8) Рассматривая полученные выражения, совместно можем получить   (6.9) Полученные соотношения называют дифференциальными зависимостями Д.И. Журавского при изгибе. Анализ дифференциальных зависимостей при изгибе по­зволяет установить некоторые особенности (правила) построения эпюр изги­бающих моментов и поперечных сил: - на участках, где нет распределенной нагрузки q, эпюры Q ограничены прямыми, параллельными базе, а эпюры М - наклонными прямыми;  - на участках, где к балке приложена распределенная нагрузка q, эпюры Q ограничены наклонными прямыми, а эпюры М - квадратичными параболами. При этом, если эпюру М строим «на сжатом волокне», то выпуклость параболы будет направлена против направления действия q, а экстремум будет расположен в сечении, где эпюра Q пересекает базовую линию; - в сечениях, где к балке прикладывается сосредоточенная сила, на эпюре ^ Q будут скачки на величину и в направлении данной силы, а на эпюре М - пе­регибы, острием направленные в направлении действия этой силы; - в сечениях, где к балке прикладывается сосредоточенный момент, на эпю­ре ^ Q изменений не будет, а на эпюре М - скачок на величину этого момента;  - на участках, где Q>0, момент М возрастает, а на участках, где Q<0, мо­мент М убывает.

10. Центральное растяжение и сжатие, внутренние силы, напряжения, расчет на прочность.

Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю. Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием)

Напряжение — это внутренне усилие N, приходящее на единицу площади A.

• =A/N

Расчет на прочность выполняется с использованием условия прочности при кручении.

Во-первых, необходимо расчетным путем определить максимальные касательные напряжения, возникающие в опасном поперечном сечении. Этот расчет производится по формуле:

Предварительно необходимо определить максимальный крутящий момент Мкр, возникающий от действия внешней нагрузки.

Крутящий момент Мкр характеризует уровень внутренних сил, возникающих в стержне и уравновешивающих внешнюю нагрузку

Чем больше значение Мкр , тем выше уровень внутренних сил, возникающих в стержне.

Прочность стержня будет определять то поперечное сечение стержня, в котором крутящий момент Мкр имеет максимальное значение.

Размерность крутящего момента - Мкр: кГсм, кГм, Нм, кНм и т.д.

После определения максимального значения крутящего момента необходимо определить характеристику поперечного сечения, определяющую прочность круглого стержня при кручении, которая называется полярным моментом сопротивления и обозначается Wр.

Таким образом, определены максимальные касательные напряжения  , которые определяют прочность стержня, но не дают ответа на вопрос, выдержит ли рассматриваемый стержень внешнюю нагрузку без разрушения или нет.

Для решения поставленной задачи еще необходимо знать допускаемые напряжения , в сравнении с которыми максимальных напряжений   и выносится решение о прочности или непрочности рассчитываемого стержня.

Определяется это с использованием условия прочности при кручении.

Таким образом, путем сравнения максимальных напряжений, возникающих в опасном сечении стержня круглого поперечного сечения  c Допускаемыми   и принимается решение о прочности стержня.

С использованием условия прочности возможно решение двух задач:

Первая задача носит название проверочной; Вторая задача называется проектировочной.

11. Деформация при растяжении. Закон Гука. Проверка жесткости при растяжении