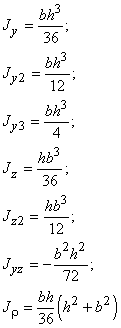задачи курса механика материалов

Создание новых конструкций, машин, приборов, должно сопровождаться временным снижением их стоимости на единицу продукции. Одной из причин отказа работоспособности является разрушение, или недопустимая деформация.

Разрушение – это непредусмотренное разрушение тела на части.

Деформация – это изменение размеров тела, или формы тела, поэтому для определения нормальной работы конструкции должны удовлетворяться условия прочности, жесткости и устойчивости.

Механика материалов – это один из разделов механики твердого деформируемого тела, целью которого являются изучение метода расчета простейших элементов конструкций.

Прочность – способность Цели элемента конструкции сопротивляться воздействию приложенных к нему сил не разрушаясь.

Жесткость – способность элемента конструкции противостоять образованию деформаций.

Устойчивость – способность элемента конструкции сохранять свою первоначальную форму упругого равновесия.

Теоретическая часть основывается на теор. Мех. а практическая на физике и материаловедении.

Объекты изучения

При всем разнообразии конструктивных элементов встречающихся в элементах и машинах их можно свести к сравнительно небольшому числу основных элементов

А) стержень

Б) оболочка

В) пластина

Г) массив

Основные определения, гипотезы и допущения курса мех мат

Идеальные материалы обладают разнообразными физическими свойствами и хар. Для них структурами.

С целью упрощения расчетов в механике материалов используют следующие допущения о свойствах.

а) материал считается однородным если его свойства во всех точках одинаковы.

б) материал считается изотропным, если его свойства во всех свойствах одинаковы

в) материал обладает свойствами идеальной упругости в следствии которой деформируемое тело полностью восстанавливает свою форму и размеры после снятия нагруки.

г) форма и размеры упругого тела меняются прямопрапорционально от воздействия нагрузки. (выполняется закон Гука)

д) материал обладает свойством сплошности ( способность заполнять пространство без пустот)

е) упругие тела являются относительно жесткими благодаря этому перемещения точек весьма малы по сравнению с размерами самого тела.

ж) поперечные сечения проведенные в теле до деформации остаются плоскими и после деформации. (Гипотеза Бернулли )

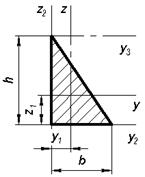
Геометрические характеристики плоских фигур

Геометрические характеристики плоских сечений

 

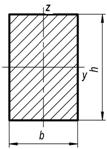
Форма сечения	Площадь сечения А	Моменты инерции: , ,	Моменты сопротивления: ,
Оси y, z – главные, центральные
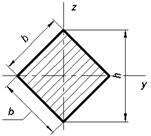
		Наибольшие касательные напряжения при кручении: посредине длинных сторон  ; посредине коротких сторон  .   Коэффициенты  ,  ,  в зависимости от соотношения сторон h/b 1 1,5 1,75 2 2,5 3 4 6 8 10 0,208 0,231 0,239 0,246 0,256 0,267 0,282 0,299 0,307 0,313 0,333 0,141 0,196 0,214 0,229 0,249 0,263 0,281 0,299 0,307 0,313 0,333 1 0,859 – 0,795 – 0,753 0,745 0,743 0,743 0,743 0,743
Оси y, z – главные, центральные
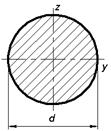
Любая центральная ось - главная
Любая центральная ось - главная
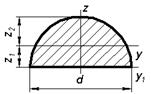
Оси y, z – главные, центральные	;	;
Оси y, z –центральные			для нижних волокон;  для верхних волокон;  для левых волокон;  для правых волокон

4. Теоретическая механика:  Центр тяжести

Смотрите также решения задач по нахождению центра тяжести в онлайн решебникахЯблонского (С.8) и Мещерского (§ 9).

Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил (Е. М. Никитин, § 42). Поэтому формулы для определения положения центра тяжести различных тел имеют вид:  x_c = (∑ G_ix_i) / ∑ G_i;  (1)y_c = (∑ G_iy_i) / ∑ G_i;  z_c = (∑ G_iz_i) / ∑ G_i.

Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес G_i каждого отрезка l_i можно представить в виде произведения  G_i = l_id,  где d – постоянный для всей фигуры вес единицы длины материала.

После подстановки в формулы (1) вместо G_i их значений l_id постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:  x_c = (∑ l_ix_i) / ∑ l_i;  (2)y_c = (∑ l_iy_i) / ∑ l_i;  z_c = (∑ l_iz_i) / ∑ l_i.

Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174), то вес каждой плоскости (поверхности) можно представить так:  G_i = F_ip,  где F_i – площади каждой поверхности, а p – вес единицы площади фигуры.

После подстановки этого значения G_i в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей:  x_c = (∑ F_ix_i) / ∑ F_i;  (3)y_c = (∑ F_iy_i) / ∑ F_i;  z_c = (∑ F_iz_i) / ∑ F_i.

Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части  G_i = V_iγ,  где V_i – объем каждой части, а γ – вес единицы объема тела.

После подстановки значений G_i в формулы (1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов:  x_c = (∑ V_ix_i) / ∑ V_i;  (4)y_c = (∑ V_iy_i) / ∑ V_i;  z_c = (∑ V_iz_i) / ∑ V_i.

При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.

Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:  (5)x_c = (r sin α)/α.

Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену  sin α = b/(2r)  и тогда  (5а)x_c = b/(2α).

В частном случае для полуокружности обе формулы примут вид (рис. 176, б):  (5б)x_c = OC = 2r/π = d/π.

Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:  (6)x_c = (2r sin α)/(3α).

Если же задана хорда сектора, то:  (6а)x_c = b/(3α).

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)  (6б)x_c = OC = 4r/(3π) = 2d/(3π).

Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.

У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).

При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:

1) выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;

2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;

3) определить или длины, или площади, или объемы составных частей;

4) выбрать расположение осей координат;

5) определить координаты центров тяжести составных частей;

6) найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;

7) по найденным координатам указать на рисунке положение центра тяжести тела.

5. Зависимость между моментами инерции относительно параллельных осей

y

x

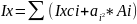
Ix, Iy – осевые центробежные моменты инерции

a,b – коэффициенты перехода между осями координат

А – площадь поперечного сечения

6. Главные оси и главные осевые моменты инерции

Оси относительно которых центробежный момент инерции равен 0, осевые моменты достигают максимальных значений ( max min) называются главными осями, а осевые моменты главными моментами инерции.

U(max) V(min)

Положение главных осей определяется углом α

Данный угол определяется :

Если угол α получился положительным, то поворот осуществляется против хода часовой стрелки, отрицательный, если по ходу часовой стрелки.

7. Внешние силы и их классификация

Внешними силами называют силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами.

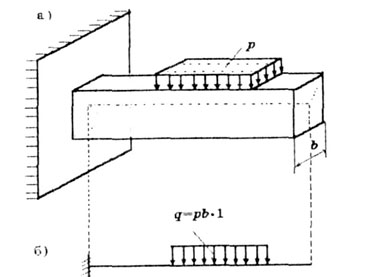
Если же нагрузка распределена по поверхности тела или его части, то такую нагрузку называютраспределенной.

В расчетной схеме нагрузку, распределенную по поверхности (рис. 1.2) приводят к плоскости, совпадающей с продольной осью, в результате чего получается нагрузка, распределенная по линии.

Мерой такой нагрузки является ее интенсивность q - величина нагрузки на единицу длины. Размерность - Н/м.

Равнодействующая распределенной нагрузки численно равна площади ее эпюры и приложена в центре ее тяжести.

Рис. 1.2

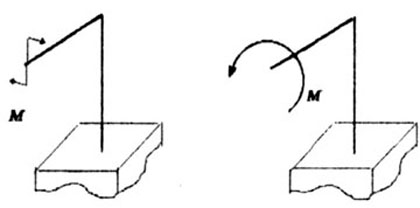
Кроме тoro, встречаются нагрузки в виде сосредоточенного момента (пары сип). Есть несколько способов изображения моментов (рис. 1.3).

Рис. 1.3

Тогда М - это крутящий момент (рис. 1.4).

Рис. 1.4

Так изображается сипа, идущая к нам.

Так изображается сила, идущая от нас.

Внешние силы: 1)Объемные - равномерно распределены по всему объему материала и приложены в центре тяжести этого объема. (сила тяжести).

2)Поверхностные - приложены на поверхности материала, на малую площадь этой поверхности. (сила приложенная в точку)

Поверхностные силы

1)Сосредоточенная сила(Р) [кгс, тс, Н] 

2)Распределенная нагрузка: а) равномерно распределенная по длине (Q) [Qгс/см, гг/м, т/м, Н/м] б)не равномерно 

3)по площади (Q) [кг/см^2, Н/м^2]

4)Внешние нагрузки - бывают временные и постоянные. Временные действуют некоторый промежуток времени, постоянные действуют на протяжение всего времени работы конструкции.

5)По характеру действия делятся на: Статические, которые прикладываются к конструкции постепенно и в дальнейшем остаются постоянными.Ускорение элементов конструкции отсутствует. Динамические - нагрузки которые изменяются за малый промежуток времени, при этом элементы конструкции получают значительные ускорения. (Удар, повторно-переменные, инертные).

6)Реакции опор - они не известны и требуют определения.