4

1.Подземная гидромеханика — наука о движении жидкостей, газов и их смесей в пористых и трещиноватых горных породах. Она является той областью гидромеханики, в которой рассматривается не дви­жение жидкостей и газов вообще, а особый вид их движения — фильтрация, которая имеет свои специфические особенности. Она является теоретической основой разработки нефтяных, газовых и газоконденсатных месторождений.

2.Системы классификаций основаны на разных принципах, учитывающих различие геохимических или гидродина­мических признаков, либо различие условия залегания, либо различие про­исхождения подземных вод и т. п. В настоящее время не существует единой общепризнанной системы классификации и даже терминологии подземных вод.

В отличие от поверхностных вод подземными называют все воды, кото­рые в том или ином состоянии находятся под поверхностью земли — в тол­ще земной коры.

Подвижные (фреатические) воды насыщенной зоны делят на два типа: 1) флюационные воды, движущиеся в карстовых и пещерных водотоках и по крупным тектоническим трещинам («флюационный» — текущий);

2) фильтрационные воды, движущиеся в относительно равномерно про­ницаемых зернистых (пористых) и мелкотрещиноватых горных породах³. Фильтрационные воды в свою очередь делятся на два типа: на «воды со свободной поверхностью» и на «артезианские воды». Воды со свободной поверхностью — это чаще всего во­ды, насыщающие породу над первым сверху водоупорным пластом, т. е. воды в пласте, имеющем водонепроницаемое ложе, но не имеющем водонепрони­цаемой кровли. При откачке воды из колодца, проведенного в такой пласт, уровень воды понижается в самом пласте, образуя свободную депрессионную поверхность.

3.Движение подземных вод зависит от действия большого числа фак­торов. Однако это не означает, что все они должны быть представ­лены в математической модели. Учет большого числа факторов может привести к созданию очень сложной модели, которую нельзя будет описать математически. Чтобы построить модель разумной сложно­сти, следует применительно к изучаемому процессу разделить дейст­вующие факторы на главные и второстепенные и последними пре­небречь. При этом обязательно имеют в виду метод расчета, которым будут пользоваться, так как возможности методов разные. Аналити­ческие методы требуют более существенного упрощения природной обстановки, чем методы математического моделирования. Деление фак­торов на главные и второстепенные относительно и зависит от степени изученности и сложности гидрогеологического объекта, характера и комплекса изучаемых процессов, практической или научной важ­ности решаемой задачи. Это означает, что для одного и того же гидро­геологического объекта можно построить различные по виду, числу и комбинациям учитываемых факторов модели.

. Движение жидкостей и газов в пористой среде происходит в весь­ма сложных условиях — наличие во многих пластах повышенных температур, высоких давлений, изменяющихся в пространстве и вре­мени, соприкасание жидкостей (нефть, вода) с различными физико-химическими свойствами, взаимодействие различных фаз (жидкой и газообразной) друг с другом и с пористой средой, выделение при фильтрации нефти пузырьков растворенного в ней газа и т. д. Основным свойством жидкостей является текучесть. Если к участку жидкости, находящейся в равновесии, приложить внешнюю силу, то возникает поток частиц жидкости в том направлении, в котором эта сила приложена: жидкость течёт. Таким образом, под действием неуравновешенных внешних сил жидкость не сохраняет форму и относительное расположение частей, и поэтому принимает форму сосуда, в котором находится. Одним из характерных свойств жидкости является то, что она имеет определённый объём (при неизменных внешних условиях). Жидкость чрезвычайно трудно сжать механически, поскольку, в отличие от газа, между молекулами очень мало свободного пространства. Давление, производимое на жидкость, заключенную в сосуд, передаётся без изменения в каждую точку объёма этой жидкости (закон Паскаля, справедлив также и для газов). Кроме того, жидкости (как и газы) характеризуются вязкостью. Она определяется как способность оказывать сопротивление перемещению одной из частей относительно другой — то есть как внутреннее трение.Когда соседние слои жидкости движутся относительно друг друга, неизбежно происходит столкновение молекул дополнительно к тому, которое обусловлено тепловым движением. Возникают силы, затормаживающие упорядоченное движение. При этом кинетическая энергия упорядоченного движения переходит в тепловую — энергию хаотического движения молекул.Жидкость в сосуде, приведённая в движение и предоставленная самой себе, постепенно остановится, но её температура повысится. Из-за сохранения объёма жидкость способна образовывать свободную поверхность. Такая поверхность является поверхностью раздела фаз данного вещества: по одну сторону находится жидкая фаза, по другую — газообразная (пар), и, возможно, другие газы.

5.Жидкости и газы движутся в продуктивных пластах в мельчайших каналах, образованных либо системой сообщающихся друг с другом пор между зернами горной породы, либо трещинами в скелете плотно­го песчаника, известняка и т. д. Такое движение в пористой и трещи­новатой среде называется фильтрацией.

В отличие от движения жидкостей и газов по трубам и в открытых руслах фильтрация имеет следующие характерные особенности: чрез­вычайно малые поперечные размеры поровых каналов, крайне малые скорости движения жидкостей, исключительно большая роль сил тре­ния вследствие вязкости жидкостей и огромных поверхностей стенок поровых каналов, о которые происходит трение жидкостей и газов при фильтрации.

Причудливая форма поровых каналов, сечения которых резко и ха­отически меняются в пространстве вследствие неправильной формы и разнообразных размеров частиц, слагающих пористую среду, делает практически невозможным точное решение уравнений движения вяз­кой жидкости в таких условиях. В связи с этим при гидродинамическом изучении фильтрации пользуются упрощенными моделями пористой среды. Такими упрощенными моделями являются идеальный и фик­тивный грунты.

Под идеальным грун­том понимается модель пористой среды, поровые каналы которой представляют собой пучок тонких цилиндрических трубок (капил­ляров) с параллельными осями. Фиктивным грунтом называется модель пористой среды, состоящая из шариков одинакового диа­метра. В конце прошлого столетия американский гидрогеолог Ч. Слихтер развил упрощенную теорию фильтрации, позволяющую сравнивать движение жидкости по поровым каналам с течением жидкости по цилиндрическим трубкам. Основываясь на модели фиктивного грунта, он рассмотрел также геометрическую задачу, позволяющую связать пористость с углами, образованными радиу­сами соприкасающихся шаров, моделирующих пористую среду, при их различной упаковке.

Простейшим геометрическим параметром, характеризующим раз­мер порового пространства, является эффективный диаметр частиц грунта. Его можно определить в результате механического анализа грунта. Эффективным диаметром частиц, слагающих ре­альную пористую среду, называется такой диаметр шаров, обра­зующих фиктивный грунт, при котором гидравлическое сопротив­ление, оказываемое фильтрующейся жидкости в реальном и экви­валентном фиктивном грунте, одинаково. Однако на практике эф­фективный диаметр зерен определить трудно (особенно для сцементированных песчаников). Поэтому теория Ч. Слихтера не нашла широкого практического применения.

6.Виды пористости:

Общая (полная , абсолютная ) пористость – суммарный объем всех пор (V_ПОР) , открытых и закрытых.

поры делятся на виды по размерам:

1.микропоры (<2 нм);

2.мезопоры (2-50 нм);

3.макропоры (>50 нм).

по размерам

-субкапиллярные (разрез пор < 0,0002 мм) – практически непроницаемые: глины , глинистые сланцы , эвапориты( соль ,гипс , ангидрит) ;

-капиллярные ( размер пор от 0,0002 до 0,5 мм);

-сверхкапиллярные >0,5 мм.

По крупным (сверхкапиллярным) каналам и порам движение нефти, воды, газа происходит свободно, а по капиллярам – при значительном участии капиллярных сил .

В субкапиллярных каналах жидкость удерживается межмолекуляными силами (силой притяжения стенок каналов ), поэтому практически никакого движения не происходит .

Породы , поры которых представлены в основном субкапиллярными каналами, независимо от пористости практически непроницаемы для жидкостей и газов (глины, глинистые сланцы).

Поры по происхождению:

-первичные

-вторичные

. 7 коэффициент пористости (или просто пористость) т, определенный для некоторого элемента пористой среды как отношение объема V_n, занятого порами в этом элементе, к его общему объему V.Обычно различают полную, открытую и эффективную пористости. При опреде­лении последней учитываются лишь соединенные между собой поры, которые могут быть заполнены жидкостью извне. При изучении процес­сов фильтрации важна именно эффективная пористостьПолная пористость - совокупность всех пор Открытая пористость- соединенные между собой поры Эфективная пористость- соединенные между собой поры, которые заполнены жидкостью(флюидом)

8. Фиктивным грунтом называется модель пористой среды, состоящей из шариков одинакового диаметра. Под идеальным грунтом пони­мается модель пористой среды, поровые каналы которой представляют пучок тонких цилиндрических трубок (капилляров) с параллельными осями. Для перехода от фиктивного грунта к естественному нужно определить величины эф­фективного диаметра частиц, слагающих реальную пористую среду. Представление о составе естественного грунта получается из данных механического анализа его

Эффектив­ным диаметром частиц, слагающих реальную пористую среду, назы­вается такой диаметр шаров, образующих фиктивный грунт, при кото­ром гидравлическое сопротивление, оказываемое фильтрующейся жид­кости в реальном и эквивалентном фиктивном грунте, одинаково. Простейший геометрический параметр, характеризующий размер порового пространства,-эффективный диаметр d₃$ частиц грунта. Он определяется в результате механического анализа грунта.

9.линейный закон фильтрации

Основное соотношение теории фильтрации - закон фильт­рации устанавливает связь между вектором скорости фильт­рации и тем полем давления, которое вызывает фильтрацион­ное течение. Первые экспериментальные наблюдения за движением воды в трубах, заполненных песком, провели французские инженеры А. Дарси (1856 г.) и Ж. Дюпюи (1848-1863 гг.)

Обозначим через Q — объемный расход жидкости через поперечное сечение рассматриваемого элемента пористого пласта, через F — пло­щадь нормального к направлению движения жидкости поперечного се­чения пласта. Тогда расход v жидкости, приходящийся на единицу по­перечного сечения пласта, определится из равенства:

Введение понятия скорости фильтрации позволяет рассматривать пласт как непрерывное поле скоростей фильтрации и давлений, ве­личина которых в каждой точке пласта является функцией коорди­нат этой точки и времени

Коэффициент фильтрации /с_ф или коэффициент проницаемости к определяют экспериментально в специальном приборе-пермеаметре, содержащем образец исследуемого грунта

Дарси закон устанавливает линейную зависимость между объемным расходом жидкости или газа и гидравлическим градиентом (уклоном, перепадом  давления) в пористых средах, например, в мелкозернистых, песчаных и глинистых грунтах. Дарси закон является эмпирическим, он адекватно описывает характер движения поровой жидкости при относительно малых градиентах давления, в том числе при фильтрации воды через грунт под плотинами и другими гидротехническими сооружениями, через стенки и дно каналов. Дарси закон обычно используют при расчетах режимов разработки нефти и газа.

Формула, выражающая линейный Дарси закон, имеет вид: 

v = Q / F = ( k / m ) (Dp / L), 

где v - скорость фильтрации жидкости или газа,

Q - объемный расход,

F - площадь поперечного сечения образца или эффективная площадь рассматриваемого объема пористой среды,

k - коэффициент проницаемости среды,

m - динамическая вязкость жидкости или газа,

Dр - перепад давления на длине среды L.

10. Под проницаемостью пористой среды понимается свойство по­ристой среды пропускать сквозь себя жидкости и газы. Следует под­черкнуть, что проницаемость (проводимость) пористой среды есть ее «динамическое свойство», проявляющееся лишь при фильтрации жид­костей или газов.

Единица проницаемости — дарси. Очевидно, что при Q — 1, µ — 1, ΔL = 1, F = 1 и Δр = 1 коэффи­циент проницаемости к = 1. Отсюда вытекает физическое определение единицы проницаемости пористой среды. За единицу проницаемости пористой среды принимается проница­емость такой пористой среды, при фильтрации через образец которой площадью в 1 см² и длиною в 1 см при перепаде давления в 1 am расход жидкости вязкостью в 1 сантипуаз составляет 1 см³/сек. Про­ницаемость такой пористой среды равна 1 дарси и в дальнейшем обо­значается д.Лабораторное определение величины коэффи­циента проницаемости Через образец породы площадью сечения F и длиною L прокачивается жидкость, абсолютная вязкость которой р (при темпе­ратуре опыта) должна быть известна. Измерив при помощи маномет­ров величину перепада давления Δр на длине L и замерив расход жидкости Q, по формуле определяют величину коэффициента проницаемости к.При лабораторном определении коэффициента проницаемости необходимо убедиться, что фильтрация жидкости происходит по ли­нейному закону фильтрации. Это легко сделать, построив график за­висимости Q = Q(Ap).лабораторное определение коэффи­циента проницаемости следует производить при помощи газа, соприка­сание которого с пористой средой не вызывает фи­зико-химических явлений. В качестве такого газа можно использовать воздух, очищенный от влаги и механических примесей.

Вопрос №11. Ламинарный и турбулентный потоки, критическая скорость движения жидкости. Число Рейнольдса.

Ламинарный поток - это поток в каждой точке которого скорость имеет одно и тоже значение.

Турбулентный поток - все части потока идут с разной скоростью, но двигаются в одном направлении.

Число Рейнольдса, при котором • ламинарный режим переходит в турбулентный, называют критическим. По исследованиям Рейнольдса ReKp— 2320. При Re<2320 движение жидкости происходит при ламинарном режиме, при Re>2320 движение жидкости происходит при турбулентном режиме. Скорость, соответствующую критическому числу Рейнольдса, называют критической скоростью. Число Рейнольдса - это безразмерная характеристика потока жидкости, определенная отношением следующих величин: динамического давления(ρu²) и касательного напряжения (μu / L),которая может быть выражена следующим образом Re = (ρu²) / (μu / L);    = ρu L /μ; = u L /ν,  где Re = Число Рейнольдса (безразмерное), ρ= плотность (кг/м³, фунт/фут³), u = скорость (м/с,фут/с ), μ = динамическая вязкость (Н*с/м², фунт/с* фут), L = характеристический размер (м, фут),ν = кинематическая вязкость (м²/с, фут ²/с)

Для каждого вида течения существует критическое число Рейнольдса, Re_κρ, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При Re < Re_κρ течение происходит в ламинарном режиме, при Re > Re_κρ возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой трубе с очень гладкими стенками 

Вопрос №12. Границы применимости линейного закона фильтрации.

Нижняя граница определяется проявлением неньютоновских геологических свойств жидкости, ее взаимодействием с твердым скелетом пористой среды при достаточно малых скоростях фильтрации. Рассмотрим каждый из этих предельных случаев, которые приводят к нелинейным законам фильтрации.

Верхняя граница применимости закона Дарси. Наиболее полно изучены отклонения от закона Дарси, вызванные проявлением инерционных сил при увеличении скорости фильтрации.

Вопрос №13. Простейшие фильтрационные потоки, их описание. Одномерные двумерные, трехмерные потоки. Плоскопараллельные и плоскорадиальные потоки.

Одномерным называется фильтрационный поток жидкости, в котором скорость фильтрации и напор являются функциями только одной координаты, отсчитываемой вдоль линии тока. К одномерным относятся следующие потоки:1) прямолинейно-параллельный фильтрационный поток2) плоскорадиальный фильтрационный поток3)радиально-сферический фильтрационный поток. Прямолинейно-параллельный поток: траектории    движения частиц жидкости, совпадающие при установившемся движении с линиями тока, являющиеся параллельными прямыми, а скорости фильтрации во всех точках любого поперечного сечения потока равны друг другу. Плоскорадиальный фильтрационный поток: Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины,  а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; поверхности равных скоростей (изотахи) и эквипотенциальные поверхности перпендикулярны траекториям. Сферически-радиальный поток в пласте больших размеров к полусферической скважине При сферически-радиальном притоке распределение давления характеризуется еще более сложной зависимостью. двухфазное течение, соответствует вытеснению жидкости, первоначально заполнявшей поры, другой жидкостью, не смешивающейся с первой. трехфазной поток имеет большое практическое значение, так как в нефтегазоносных пластах при определенных условиях происходит совместное движение нефти, воды свободного газа.

Вопрос№14. Гидродинамические различия скважин, отличающихся характерном вскрытиям пласта. Высотные, гипсометрические отметки. Напоры, приведенные давления.

несовершенные скважины, вскрывшие пласт не полностью (скважины, несовершенные по степени вскрытия), а также скважины, сообщающимися с пластом через перфорационные каналы искусственного фильтра (скважины, несовершенные по характеру вскрытия).

гидродинамически совершенные скважины - вскрывших пласт на всю толщину и сообщающихся с пластом по всей площади живого сечения забоя скважины. Высота Н, характеризующая вертикальное расстояние поверхности кровли пласта в какой-либо точке от уровня моря, называется гипсометрической отметкой кровли пласта в этой точке. Напор, в гидравлике и гидродинамике — давление жидкости, выражаемое высотой столба жидкости над выбранным уровнем отсчёта. Под приведенным давлением понимается "давление жидкости, приведенное к определенной плоскости сравнения. Приведенное давление P n p складывается из пластового давления в определенной точке водоносного горизонта Pi и давления столба воды, замеряемого от данной точки до плоскости сравнения.

Вопрос №15. Гидродинамические особенности фильтрационных потоков. Основные элементы гидродинамических потоков. Краевые и граничные условия. Мощность, напор потока, гидравлический уклон, линии токов, падения напоров, и т.п. Определение основных гидродинамических характеристик.

Фильтрационным потоком обычно называют условный поток, проходящий через всю породу. Реальный поток фильтруется по открытым ( сообщающимся) порам и трещинам. В качестве граничных условий используют значения напоров, расходов или скоростей фильтрации на границах потока. Граничные условия первого рода наблюдаются на границах подземных потоков с поверхностными водотоками, уровень воды в которых либо не изменяется - cons t (контуры постоянного напора), либо изменяется по какому-нибудь закону (контуры переменного напора).

16. Эквипотенциали. Гидроизогипсы. Гидродинамическая сетка фильтрационного потока, ее свойства, правила построения. Направление движение потока характеризуется линиями токов, которые совпадают с траекториями движения частиц жидкости фильтрационного потока.

Линии перпендикулярные линиям токов, представляют собой линии равных напоров, или эквипотенциали (линии равных потенциалов) В пространственном потоке рассматривают не линии, а поверхности равных напоров. Поверхности и линии равных напоров обладают таким свойством, что пьезометрические напоры во всех их точках равны. Проекции линий равных напоров на горизонтальную плоскость представляет собой гидроизогипсы (для грунтовых вод) или гидроизопьезы (для напорных вод).

Совокупность взаимно ортогональных линий токов и линий равных напоров представляет собой гидродинамическую сетку фильтрационного потока. В условиях установившегося движения гидродинамическая стека потока постоянная, в условиях неустановившегося движения – переменная. Простейшим примером гидродинамической сетки является сетка напорного потока в условиях однородного пласта постоянной мощности при горизонтальном водоупоре. В таких условиях гидродинамическая стека представляет собой совокупность взаимно ортогональных горизонтальных и вертикальных линий и состоит из равных квадратных и прямоугольных ячеек. В других условиях линии токов и равных напоров могут быть криволинейными, а ячейки гидродинамической сетки соответственно криволинейными квадратами, прямоугольниками и трапециями.

Гидродинамические сетки потоков получают либо экспериментально, либо путем их графического их построения.

При построении сеток следует учитывать некоторые общие рекомендации.Линии токов и линии равных напоров должны быть плавными, взаимно перпендикулярными линиями. При построении линий токов у границ слоев с разными фильтрационными свойствами следует учитывать закон преломления фильтрационных токов.

1. Общее кол-во линий токов и линий равных напоров устанавливается в зависимости от принятого масштаба построения сетки, требуемой точности и особенностей условий фильтрации.

2. В переделах каждой лены тока (участок потока выделенный двумя соседними линиями тока) должно соблюдаться условие комфортности ее ячеек, вытекающее из постоянства расхода вдоль ленты тока

3. Все проницаемые поверхности являются линиями токов, а проницаемые, как правило, линиями равны напоров.

Гидродинамические сетки используются для качественной и количественной оценки потоков подземных вод. Имея гидродинамическую сетку потока, можно легко определить все его основные элементы: напоры, напорные градиенты, скорость фильтрации, рсход потока.

17. Одномерное движение несжимаемой жидкости по линейному закону фильтрации

В зависимости о формы и характера границ в плане и в разрезе создаются разнообразные по виду и структуре потоки подземных вод. Для удобства рассмотрения гидродинамических особенностей потоков водится понятие мерности потока, отражающее его вид и структуру. Так как скорость фильтрации – вектор, то мерность потока оценивается по числу составляющих скорости фильтрации. Выделяются потоки с одной составляющей – одномерные, с двумя – двухмерные, с тремя – трехмерные.

В реальных природных условиях, строго говоря, потоки подземных вод являются трехмерными.

В плоских в плане течениях горизонтальные составляющие скорости фильтрации по вертикали или напорные градиенты осредняются и считаются одинаковыми. Вертикальные составляющие скорости фильтрации ввиду их малости во внимание не принимаются. Акая предпосылка известна в динамике подземных вод, как предпосылка Дюпюи. Плоские потоки имеют широкое распространение в природе. Примерами плоских в плане потоков является движение подземных вод в районах инженерных сооружений, потоки речных долин и междуречий; примерами потоков плоских в разрезе является фильтрация воды под плотиной, движение воды по пластам в условиях их гидравлической взаимосвязи и другие виды профильных потоков.

Если в плоском потоке прямолинейные линии токов параллельны одна другой, поток называют плоскопараллельным или линейным, одномерным. Линейный одномерный поток наблюдается, например, при фильтрации воды через междуречный массив из одной речной долины в другую при параллельном их расположении или же при движении естественного напорного потока по однородному пласту постоянной мощности

18. Плоское радиальное движение по линейному закону. Индикаторная диаграмма

Если линии токов направлены по радиусам, то поток является радиальным и могут быть сходящимися или расходящимися по направлению движения потока. Направление движение потока характеризуется линиями токов, которые совпадают с траекториями движения частиц жидкости фильтрационного потока. Радиальный поток имеет место на участке излучины реки или при движении воды к скважине.

19. Плоский радиальный фильтрационный поток к гидродинамический совершенной скважине

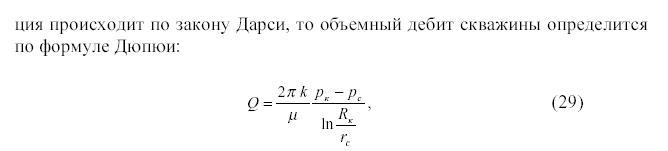
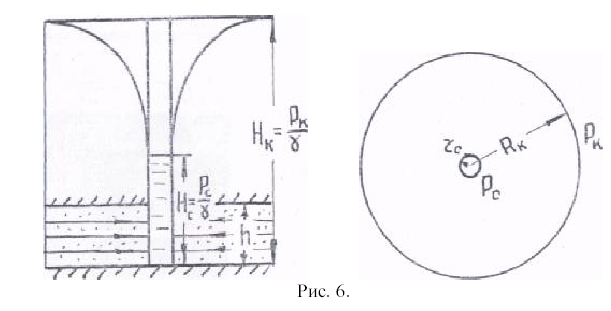
20. Движение жидкости со свободной поверхностью к скважине. Формула Дюпюи.

ФОРМУЛА ДЮПЮИ - определяет дебит гидродинамически совершенной скважины при плоско-радиальном подтоке к ней однородной несжимаемой жидкости в условиях напорного режима и линейного закона фильтрации

где k-коэффициент проницаемости, дарси; h - мощность пласта, см; Р_к и Р_с-давление на контуре питания и в скважине, ат; R_к и R_с-радиусы контура питания и скважины, см; μ - вязкость жидкости, сантипуазы; Q_r - дебит скважины, см³/сек. Ф. Д. широко применяется в нефтепромысловом деле.

При получении решений для естественных потоков часто используется схема однородного по вертикали безнапорного потока на горизонтальном водоупоре. Вертикальные составляющие скорости фильтрации потока не учитываются ввиду их незначительности, а горизонтальные принимаются постоянными по глубине в каждом сечении (предпосылка Дюпюи.)

По Трунову Q = k*h²₁ – h²₂/2M lД

Движение жидкости может быть плоскопараллельным, плоскорадиальным.

В естественных условиях движение вод может быть равномерными и неравномерным. При равномерном движении скорость потока по пути движения неизменна. Такой вид может иметь место при фильтрации напорного потока через пласт постоянной мощности или при фильтрации безнапорного потока в наклонных водоносных пластах. Обычно же движение вод неравномерное, поскольку скорость фильтрации изменяется от сечения к сечению. В однородных пластах это происходит в связи с изменением мощности, ширины и расхода потока, в неоднородных

дополнительно за счет изменения фильтрационных свойств.

24. Анизотропия проницаемости и взаимодействие скважин.

Анизотропи́я (от др.-греч. — неравный ,и — направление) —неоднородность( неодинаковость) с Проницаемость - способность горных пород фильтровать сквозь себя флюиды при наличии перепада давления. и свойств среды. В пласте жидкость в основном движется по трещинам, пронизывающим породу во всевозможных направлениях, каждое из которых не имеет никаких преимуществ перед остальными. Теория анизотропных сред в подземной гидродинамике наиболее полно развита для слоистых горных пород, когда главные направления проницаемости (вдоль и поперек напластования) заранее известны. Увеличение эффективного давления при постоянной температуре приводит к уменьше­нию проницаемости.

25. Взаимодействие скважин. Простейшие варианты взаимодействия скважин.

- влияние откачки воды из одной скважины или колодца на другие, близ расположенные.

Так откачка воды из одной скважины (или колодца) влияет на другие, выражающееся в том, что воронки депрессий, создаваемые откачкой, частично перекрывают одна другую, вследствие чего производительность каждой скважины (колодца) падает.

(Изменение дебитов нефтяных, газовых и водных скважин или их забойных давлений или тех и других одновременно под влиянием изменения режима работы окружающих скважин. )

Взаимодействие скважин имеет огромное значение при решении ряда задач, связанных с нахождением необходимого числа скважин и наивыгоднейшим их размещением на площади ()

31.Методы увеличения нефтеотдачи пластов(МУН)