Канальный или логический уровень.
Основная задача канального уровня – организовать «надежную» доставку данных по «ненадежному» каналу связи.
При рассмотрении канального уровня опишем систему при помощи следующей упрощенной модели (Рис. 3):
Передающая сторона
Приемная сторона
И
(источник)
П
(получатель)
Канальный
уровень
Канальный
уровень
К
К
Ф
Ф
физическая
среда
канал
физическая
среда
Рис. 3 Схема преобразования семиуровневой модели к упрощенному варианту
На рис.3 показан процесс преобразования семиуровневой модели к упрощенному варианту. Из рисунка видно, что все уровни выше канального считаем Источником на передающей стороне. А на приемной – Получателем. Физическую среду и физический уровень считаем Каналом.
Таким образом, при рассмотрении канального уровня можно перейти к более простой модели, представленной на Рис. 4
И
П
Кан.
ур.
Кан.
ур.
КАНАЛ
=
Рис.4 Упрощенная модель системы
При
совместной работе Источника, Канального
уровня и Получателя требуется, чтобы
данные, формируемые на выходе Источника
,
совпали
с данными, поступающими к Получателю,
даже если данные на выходе канального
уровня Источника
не совпадают с данными на входе канального
уровня Получателя
.Если
же не возможно обеспечить совпадение
и
(данных
на Источнике и Получателе), то обе этом
необходимо сообщить Получателю.
Рассмотрим простейший частный случай решения такой задачи (рис. 5):
И
КАНАЛ
кодер
декодер
П
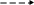
(рис.5)
Пусть Источник формирует двухбитные сообщения . Будем предполагать, что в канале может исказиться только один бит в сообщении. Задача декодера определить были ли ошибки в канале или нет.
Такую задачу можно решить следующим образом. Добавляем в сообщение один дополнительный символ (проверочный бит). Проверочный бит добавляем таким образом, чтобы число единиц в сообщении было четным, либо равным нулю. Таким образом, на выходе кодера формируются сообщения длиной в три бита . В Канал передается одно их четырех возможных сообщений, каждому из которых соответствует одно из сообщений Источника.
Декодеру известен алгоритм работы кодера, но не известно, какое из 4-х сообщений передавалось. Предположим, что мы хотим передать сообщение = (01). В результате работы кодера в канал передается сообщение = (011). Допустим, из-за искажений, возникающих в канале, произошла ошибка в старшем бите сообщения . Таким образом, к декодеру поступило искаженное сообщение = (111):
= (0 1) – сообщение на выходе источника
= (0 1 1)- сообщение на выходе кодера
=
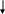(0* 1 1) - *
ошибка в канале (в примере ошибка третьего
разряда)
= (1 1 1) – сообщение на входе декодера
На рисунке проиллюстрирован рассмотренный пример.
И
КАНАЛ
кодер
декодер
П
Декодер принимает последовательность , считанную с канала, и определяет, принадлежит ли эта последовательность множеству А ({A} - множество всех возможные сообщения на выходе кодера). Если сообщение не принадлежит этому множеству, то декодер выносит решение о том, что произошла ошибка. В рассматриваемом примере, для решения этой задачи достаточно посчитать количество единиц в принятой последовательности . Если число единиц 1 или 3 (нечетное), то выносится решение об обнаружении ошибки.
Кратно данный способ можно описать следующим образом: кодер всегда передает в канал последовательность, которая содержит четное количество единиц, декодер выносит сообщение о том, что в канале произошла ошибка, если число, принятой последовательности, будет нечетное.
Вышерассмотренный способ называется кодом с проверкой на честность.
Покажем, что код с проверкой на честность не всегда сможет обнаружить две ошибки (рис. 6):
Пусть
на выходе Источника формируется сообщение
.
В соответствии с рассмотренным выше
алгоритмом, в канал поступает сообщение
.
Из-за
ошибок, возникающих в канале, на входе
декодера поступает сообщение
.
Видено, что в канале произошли две ошибки
– в старшем и младшем разрядах сообщения
.
И
КАНАЛ
кодер
декодер
(рис.6)
Декодер
проверяет количество единиц в принятом
сообщении
на
четность и выносит решение, что ошибок
не было. Однако при этом Получатель
получит сообщение
,
которое
не соответствует переданному Источником
.
Существуют более совершенные способы формирования избыточных разрядов (дополнительных бит), которые позволяют обнаруживать более чем одну ошибку. Они используются при передаче сообщений по менее надежным каналам.
Теперь рассмотрим следующую задачу: требуется так организовать совместную работу кодера и декодера, чтобы сообщение от Источника до Получателя было доставлено без ошибок.
Примем следующие допущения:
По-прежнему есть Источник, который может передать любую двух битную последовательность.
Используется код с проверкой на четность.
Имеется прямой канал от Источника к Получателю, в прямом канале может происходить только одна ошибка при передаче последовательности из трех бит.
Имеется обратный канал от Получателя к Источнику, по которому можно передавать только один бит (сообщение об обнаруженной ошибке - квитанция).
Ошибок в обратном канале не происходит.
Модель такой системы представлена на Рис. 7
И
КАНАЛ
кодер
декодер
П
КАНАЛ
обр.
Рис. 7
Требуется так организовать совместную работу кодера и декодера, чтобы сообщение от Источника до Получателя было доставлено без ошибок. Исходим из предположения, что в канале ошибки возникают случайно.
Передающая сторона (Источник и кодер) работает по следующему алгоритму:
Кодер принимает сообщение от Источника;
Передает закодированное сообщение по каналу;
Принимает квитанцию
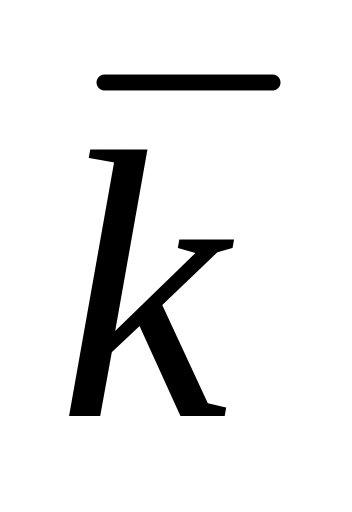от
обратного канала;Если принятая от Получателя квитанция равна нулю
(ошибки нет), то возвращается в п. 1. для
следующего сообщения. Если квитанция
равна единице
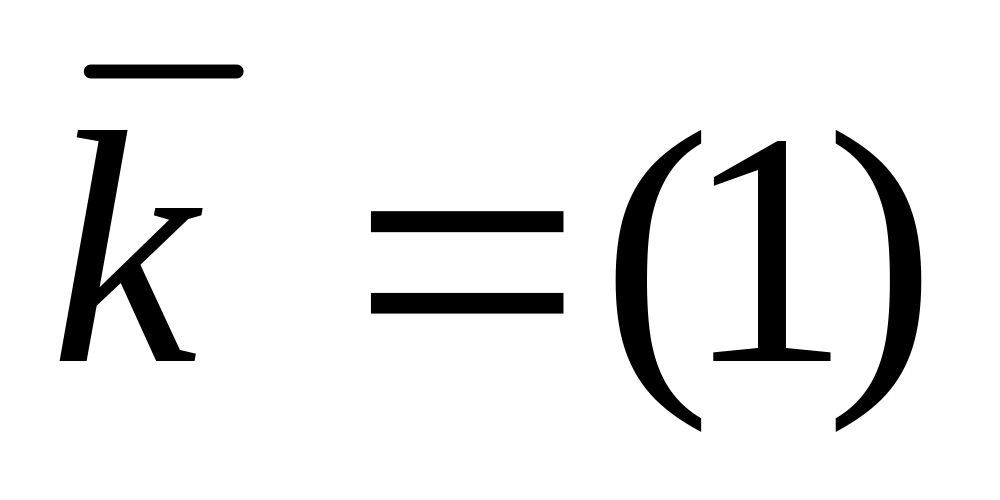(ошибка есть), то возвращается в п. 1. для
текущего сообщения.
Приемная сторона (декодер и Получатель) работает по следующему алгоритму:
Декодер принимает данные из прямого канала и определяет, есть ошибки или нет;
Если ошибок нет, то передает данные Получателю, а по обратному каналу отправляет квитанцию, разную нулю .
Если ошибка есть, то отправляет Источнику по обратному каналу квитанцию, содержащую 1 , а Получателю отправляется сообщение об ошибке.
Для того чтобы выяснить сколько времени потребуется для передачи одного сообщения, введем в рассмотрение следующую вероятную модель.
Предположим, что в прямом канале события, связанные с тем, что произошла ошибка, происходят с вероятностью Р а сообщения, связанные тем, что ошибка не произошла, происходит соответственно с вероятностью (1-Р).
Введем случайную величину N равную числу передач, которые необходимо сделать для того, чтобы сообщение было успешно передано.
N
может принимать следующие значения: N
= 1, 2, 3,…,
Выясним, чему равняется математическое ожидание количества передач N (M [N]), т.е. сколько в среднем придется сделать передач, до того момента, когда сообщение будет удачно передано.
Pr – от англ. сл. вероятность. В {…} – событие, вероятность которого следует вычислить.
Pr {N=1}=1-P – вероятность одной передачи.
Pr {N=2} = Pr {вероятность события, что первая передача с ошибкой, а вторая передача без ошибки}= P* (1-P)
Pr {N=3} = Pr {вероятность события, что первая передача с ошибкой, вторая– с ошибкой, третья– без ошибки}= P * P * (1-P)
.
.
.
В общем случае вероятность того, что потребуется i - попыток.
Pr {N=i} = P (i-1)* (1-P)
Тогда математическое ожидание количества необходимых передач:
Равенство № 1 получено на основе свойства производных.
Равенство № 2 получено на основе геометрической прогрессии.
Среднее
число передач, затраченных на передачу
одного сообщения M[N]=(p)
посмотрим на (рис.8). Если при передаче
нет ошибок, то
,
если есть ошибки, то при увеличении P
.
M[N]
1
P
0
1
Рис.8 Зависимость среднего числа передач от вероятности появления ошибок в канале.
Общий вывод: организовать безошибочную доставку сообщений от источника к получателю по каналу с ошибками можно за счет использования следующих приемов:
За счет внесения избыточности в передаваемое сообщение (в рассмотренном примере передаваемым двум битам, добавляется один проверочный бит, что позволяло обнаружить однократные ошибки);
За счет использования квитанций, передаваемых по обратному каналу для организации повторных передач.
Данный способ позволяет при любой отличной от единицы вероятности ошибки организовать надежную доставку сообщения от источника к получателю. При этом ухудшения характеристик канала приводит к увеличению вероятности ошибки, что в соответствии с формулой для M [N] приводит к увеличению числа повторных передач и, следовательно, увеличивается время доставки при передаче данных.