Уравнение касательной

Ключевые слова: касательная, прямая, производная, функция, угловой коэффициент

Производной функции f(x) в точке x₀ называется предел отношения приращения функции в этой точке f=f(x0+ x)−f(x0) к приращению аргумента x при x 0: f (x0)=lim x 0( xf(x0+ x))/f(x0).

Геометрический смысл производной

Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Билет 31

Инвариантность формы первого дифференциала

Поскольку u '(x0) dx = du, то формулу (1) можно представить в виде

 

d f(u) = f '(u0) du.

 

Последняя формула показывает, что дифференциал функции выражается формулой одного и того же вида (одной и той же формы), как в случае функции независимой переменной, так и в случае функции от функции. Это свойство дифференциала называют инвариантностью формы.

Билет 32

Производная обратной функции

Пусть - функция от аргумента x в некотором интервале . Если в уравнении y считать аргументом, а x - функцией, то возникает новая функция , где - функция обратная данной.

Теорема (о дифференцировании обратной функции)

Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е

Билет 33

Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

Билет 34

Производные и дифференциалы высших порядков

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом, f"(x) = (f'(x))'.

Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,

f⁽ⁿ⁾(x) = (f^(n-1)(x))',   n ϵ N,   f⁽⁰⁾(x) = f(x).

Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dⁿf(x) = d(d^n-1f(x)),   d⁰f(x) = f(x),   n ϵ N.

Если x - независимая переменная, то dx = const   и   d²x = d³x = ... = dⁿx = 0.

В этом случае справедлива формула dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ.

Формула Лейбница для -ой производной произведения двух функций — обобщение правила дифференцирования произведения (и отношения) двух функций на случай -кратного дифференцирования.

Пусть функции и  — раз дифференцируемые функции, тогда

где 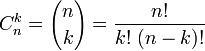 — биномиальные коэффициенты.

Билет 35

Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

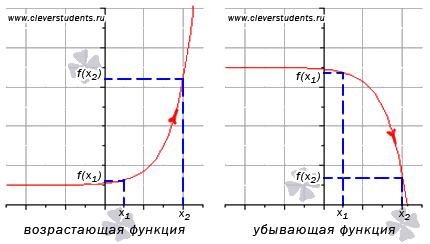
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.

Необходимое условие экстремума.

1. Функция одного переменного. Пусть х₀ – точка экстремума (максимума или минимума) функции у = f(x). Тогда в этой точке производная  равна нулю или не существует.

2. Функция многих переменных. Пусть   равны нулю (i = 1, 2, …, n), либо хотя бы одна из них не существует.

Первое достаточное условие экстремума. если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то - точка максимума;

если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума.

Локальный экстремум.

Слово «локальный» подчеркивает, что речь идет об экстремуме функции в достаточно малой окрестности рассматриваемой точки. Таким образом, локальный максимум (минимум) – это наибольшее (соответственно наименьшее) значение функции в некоторой достаточно малой окрестности рассматриваемой точки.

Заметим, что речь может идти как о функции одного, так и нескольких переменных.

Для соответствующих глобальных характеристик вместо слов «экстремум», «максимум», «минимум» обычно употребляют термины «наибольшее значение функции» и «наименьшее значение функции» на соответствующем множестве.

Билет 36

Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если f(a) = f(b)

то внутри интервала [а, b] найдется хотя бы одно такое значение x₀ (a < x₀ < b), что f ' (x₀) = 0.

  Доказательство. Рассмотрим два случая.   1. Функция f(x) постоянна на интервале [а, b]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически.   2. Функция f(x) не является постоянной (Рисунок 1); тогда наибольшего или наименьшего или обоих этих значений она достигает во внутренней точке интервала, ибо f(b) = f(a), и если f(a) - наименьшее значение, то наибольшее значение значение функция f(x) примет внутри интервала.

Рис.1

  Пусть например f(x₀) - наибольшее значение функции f(x) на интервале [а, b] и x₀ - внутренняя точка этого интервала. Тогда f(x₀) является максимумом функции: f(x₀)  f(x) для всех x из достаточно малой окрестности x₀ [за эту окрестность можно впрочем, взять интервал (а, b)].   Так как, по условию, f(x) имеет в точке x₀ производную, то по теореме о необходимом признаке экстремума,

f ' (x₀) = 0,

и теорема Ролля доказана.

Билет 37

 Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f(b) - f(a) = (b - a)f '(x).

  Доказательство. Рассмотрим вспомогательную функцию

F(x) = f(x) - k(x - a),

где - угловой коэффициент хорды AB (смотри рисунок 2).   Эта функция удовлетворяет всем условиям теоремы Ролля.   В самом деле, при x = a имеем F(a) = f(a) - k(a - a) = f(a), при x = b имеем

  Кроме того, так как функция f(x) и k(x - a) непрерывны на [a, b] и диференцируемы в (a, b), то и функция F(x) = f(x) - k(x - a) непрерывна на [a, b] и диференцируема в (a, b).   Следовательно, по теореме Ролля, в интервале (a, b) найдется такая точка x₀, что

F'(x₀) = 0,

т.е.

f ' (x₀) - k = 0

или

  Отсюда имеем

f(b) - f(a) = (b - a)f ' (x₀),

что и требовалось доказать.   Так как a + (b - a) = b, то величина a + (b - a), где Q - правильная положительная дробь (0 <  < 1), равна какому-то числу в интервале (a, b), поэтому формулу Лагранжа можно записать в виде

f(b) - f(a) = (b - a)f ' [a + (b - a)]

  Если положить a = x, b = x + x, откуда b - a = x, то формула Лагранжа запишется в виде

y = f(x + x) - f(x) = xf ' (x + x).

  Ранее было доказано, что если функция равна постоянной C при любом значении x в интервале (a, b), то ее производная равна нулю.   Докажем теперь обратную теорему, являющуюся следствием теоремы Лагранжа:   Если произвоодная f ' (x) обращается в нуль для любых значений x в интервале (a, b), то в этом интервале f(x) = C.   В самом деле, если x₁ и x₂ - два любых значения в интервале (a, b), то в силу теоремы Лагранжа, имеем

f(x₂) - f(x₁) = (x₂ - x₁)f'(x₀),

где, x₁ < x₀ < x₂. Но так как f'(x₀) = 0, то

f(x₂) - f(x₁) = 0,

что и доказывает нашу теорему.

Билет 38

Теорема Коши

Теорема 15. (Коши об отношении приращения двух функций) Пусть функции y = f(x), y = g(x) непрерывны на отрезке и дифференцируемы на интервале (a, b), причем g ' (x) ≠ 0 на (a, b).

Тогда существует число c (a,b) такое, что

Доказательство

Заметим, что g(b) ≠ g(a). (Если g(b) = g(a), то, по теореме Ролля, существует число c (a,b) такое, что g ' (c) = 0.)

Введем обозначение: .

Рассмотрим функцию , которая непре-рывна на [a,b], дифференцируема на (a, b) и F(a) = F(b) = 0, т.е. функция F удовлетворяет условиям теоремы Ролля.

Следовательно, существует число c (a,b) такое, что F ' (c) = 0.

Так как

Теорема доказана

Билет 39.