
- •Локальные
- •Первая теорема Вейерштрасса
- •10. Непрерывность элементарных функций
- •Первый замечательный предел
- •Второй замечательный предел
- •Уравнение касательной
- •Производная обратной функции
- •Теорема (о дифференцировании обратной функции)
- •Производные и дифференциалы высших порядков
- •Точная формулировка
- •Отношение бесконечно малых
- •Точная формулировка
- •Отношение бесконечно больших
Билет 20
Локальные
Функция, непрерывная в точке
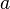 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки.Если функция
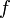 непрерывна
в точке
и
непрерывна
в точке
и
 (или
(или
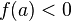 ),
то
),
то
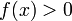 (или
(или
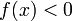 )
для всех
)
для всех
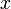 ,
достаточно близких к
,
достаточно близких к
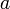 .
.Если функции и
 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции
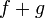 и
и
 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
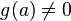 ,
то функция
,
то функция
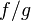 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
 ,
то их композиция
,
то их композиция
 непрерывна
в точке
.
непрерывна
в точке
.
Билет 21
Первая теорема Вейерштрасса
Если
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
то она ограничена на данном отрезке.
Замечание:
на интервале
,
то она ограничена на данном отрезке.
Замечание:
на интервале
![]() функция
может быть не ограничена.
функция
может быть не ограничена.
![]() .
.
Доказательство.
Предположим,
что
непрерывна,
но неограниченна:
![]()
![]() .
.
По
лемме Больцано-Вейерштрасса,
из последовательности
![]() можно
извлечь частичную последовательность
можно
извлечь частичную последовательность
![]() ,
сходящуюся к пределу
,
сходящуюся к пределу
![]() :
:
![]() .
По теореме о предельном переходе в
неравенстве
.
По теореме о предельном переходе в
неравенстве
![]() .
Так как
.
Так как
![]()
![]() ,
,
![]() .
Мы пришли к противоречию.
.
Мы пришли к противоречию.
То
есть
![]() -
ограничена.
-
ограничена.
![]() .
.
Билет 22
(Вторая теорема Вейерштрасса).
Если
функция
непрерывна
на отрезке
,
то она достигает свои точные верхнюю и
нижнюю грани.
![]()
Эта теорема означает, что достигаемые sup и inf означают соответственно max и min функции.
Доказательство.
Докажем,
что достигается sup (inf - аналогично).
Предположим, что
![]() на
отрезке
.
Рассмотрим вспомогательную функцию
на
отрезке
.
Рассмотрим вспомогательную функцию
![]() ,
которая непрерывна (знаменатель
,
которая непрерывна (знаменатель
![]() )
и ограничена (по теореме 13.1)
на
:
)
и ограничена (по теореме 13.1)
на
:
![]() .
.
![]() ,
,
![]() .
Таким образом
.
Таким образом
![]() .
Но M -
наименьшая
из верхних граней, а мы пришли к
противоречию, т. к.
.
Но M -
наименьшая
из верхних граней, а мы пришли к
противоречию, т. к.
![]() -
тоже верхняя грань. Теорема доказана.
-
тоже верхняя грань. Теорема доказана.
Билет 23


Билет 24.
Теорема
3.11
Пусть
![]() --
непрерывная монотонная функция,
--
непрерывная монотонная функция,
![]() ,
,
![]() .
Тогда обратная к
функция
.
Тогда обратная к
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() .
.
Доказательство.
Во-первых, заметим, что если
![]() ,
,
![]() ,
то
,
то
![]() .
.
Во-вторых,
пусть
![]() ;
рассмотрим функцию
;
рассмотрим функцию
![]() ,
которая определена при
,
которая определена при
![]() .
Очевидно, что
.
Очевидно, что
![]() --
непрерывная на
--
непрерывная на
![]() функция,
поэтому она принимает наименьшее
значение
функция,
поэтому она принимает наименьшее
значение
![]() в
некоторой точке
в
некоторой точке
![]() :
:
![]()
Таким
образом, если
![]() ,
то
,
то
![]() ,
то есть если
,
то есть если
![]() ,
то
,
то
![]() .
Последнее утверждение можно
переформулировать так: для любого числа
.
Последнее утверждение можно
переформулировать так: для любого числа
![]() найдётся
число
найдётся
число
![]() ,
такое что при
,
такое что при
![]() выполняется
неравенство
выполняется
неравенство
![]() .
(При этом
.
(При этом
![]() ,
,
![]() ,
,
![]() ,
,
![]() .)
Получили, что функция
удовлетворяет
определению равномерной непрерывности
на отрезке
;
тем самым доказано утверждение теоремы.
.)
Получили, что функция
удовлетворяет
определению равномерной непрерывности
на отрезке
;
тем самым доказано утверждение теоремы.
Билет 25
Суперпозиция
непрерывных функций.
Теорема.
Пусть функция![]() определена
в промежутке
определена
в промежутке![]() а
функция
а
функция![]() —в
промежутке
—в
промежутке![]() ,
причем значения последней функции не
выходят за пределы
,
причем значения последней функции не
выходят за пределы![]() когда
когда
![]() изменяется в
изменяется в![]() .
Если
.
Если![]() непрерывна
в точке
непрерывна
в точке![]() из
из![]() а
а![]() непрерывна
в соответствующей
точке
непрерывна
в соответствующей
точке![]() из
из![]() ,
то и сложная функция
,
то и сложная функция
![]() будет
непрерывна в точке
будет
непрерывна в точке![]()
Доказательство.
Зададимся произвольным числом![]() Так
как
Так
как
![]() непрерывна
при
непрерывна
при![]() то
по ε найдется такое
то
по ε найдется такое![]() что
что![]()
С
другой стороны, ввиду непрерывности![]() при
при
![]() .
по
найдется такое
.
по
найдется такое
![]() что
что
![]()
По
самому выбору числа
![]() отсюда следует, далее,
отсюда следует, далее,![]()
Этим
«на языке
![]() и доказана непрерывность функции
и доказана непрерывность функции![]() в точке
в точке![]()
Например,
если степенную функцию![]() представить
в виде функции
представить
в виде функции![]()
которая получается от суперпозиции логарифмической и показательной функций, то из непрерывности последних двух функций уже будет вытекать непрерывность степенной функции.
Билет 26
