5. Числа и действия над числами

1,2,3,...,8,...,424,...к..., где к - любое целое положительное число, называются натуральными числами. Целые положительные и отрицательные, а также дробные числа вида где m и n - целые числа, причем n  0, именуют числами рациональными. Всякое рациональное число можно представить конечной или, в соответствующих случаях, периодической бесконечной десятичной дробью.

Наряду с рациональными существуют иррациональные, представляющие собой непериодические бесконечные дроби. Таковы, например, = 1,4142....;  = 3,1415..., е = 2,718281...

Рациональные и иррациональные числа составляют класс действительных (вещественных) чисел.

Развитие алгебры, связанное с необходимостью извлечения квадратных корней из отрицательных чисел, потребовало введение чисел нового вида, названных комплексными. Комплексные числа представляют собой пары чисел вида a + bi, где i² = -1, то есть i = . В комплексном числе a и b - обыкновенные действительные числа, а bi именуется мнимой частью комплексного числа.

В некоторых случаях оказывается необходимым при действиях с обыкновенными вещественными числами, не обращать внимание на их знак. Тогда используется понятие об абсолютной величине или о модуле действительного числа. Модуль действительного числа обозначают символом  a . Согласно определению, например, -2 = 2 = 2; -56 = 56 и т.д.

Число (точнее говоря - переменную величину) называют бесконечно большим и обозначают символом , если желают выразить, что оно превосходит любое другое число. Этим обозначением оно не фиксируется, как объект расчетов и к символу  нельзя применять обычные правила вычислений.

Число называют бесконечно малым, если желают выразить, что оно имеет абсолютную величину меньшую, чем любое произвольно заданное (положительное) число. Для обозначения этого понятия не пользуются специальным символом, заменяя его записями вида или , читая первое из выражений так: «предел величины при x, стремящемся к бесконечности, равен нулю», а второе - «предел величины при x, стремящемся к нулю, равен бесконечности». Символ lim означает «предел», «лимит».

Совокупность действительных чисел образует линию, называемую «числовой осью», на которой каждое число служит координатой, определяющей положение точки, соответствующей числу. Числовая ось - прямая, то есть одномерное числовое пространство.

На числовой оси могут быть выбраны: начальная точка отсчета, условно принимаемое за положительное направления и масштаб. Можно считать, например, что начальная точка отсчета - «ноль», направо от нее размещены точки, отображающие положительные числа («положительное направление оси»), налево - точки, соответствующие отрицательным числам («отрицательное направление оси»).

Если некоторые объекты или свойства их представляют рядом отдельных, дискретных значений чисел, то положение каждого такого числа в своем ряду может быть обозначено индексом. Пусть, например, ряд является последовательностью чисел 15; 4,3; 2; 0,5 и и.д. Символически его можно записать так: а₁ , а₂ , а₃ , а₄ , ..., где а₁ = 15, а₂ = 4,3, а₃ = 2, а₄ = 0,5 ... Здесь числа 1, 2, 3, 4, ... определяют места членов ряда и называются индексами. Любой член ряда можно обозначить символом а_i , причем индекс i укажет его «номер» в последовательности ряда. В некоторых случаях, когда следует проводить расчеты с группами последовательно расположенных в ряд чисел, пользуются обозначениями «от а_i , до а_j ». Если указать, например, « от i = 1 до j = 8», то это означает, что следует брать группу членов ряда от 1-го до 8-го включительно.

Для условного обозначения чисел, значение которых заранее известны, обычно применяют первые буквы латинского алфавита, а для неизвестных чисел - последние (x, y, z, u, ...). Некоторыми буквами принято обозначать константы (  = 3,14... - отношение длины окружности к диаметру, e = 2,71... - основание натуральных логарифмов, g = 9,81 м.сек² = величина ускорения тела, падающего в пустоте под действием земного притяжения, и т.д.).

Над числами наиболее часто выполняют следующие операции: сложение, вычитание, умножение и деление, возведение в степень, извлечение корня, логарифмирование. Правила 4-х арифметических действий общеизвестны, поэтому напомним только об операциях возведения в степень, извлечения корня и логарифмирования.

При возведении в степень число («основание степени») умножается само на себя столько раз, сколько указано «показателем степени». Возведение во вторую степень (в квадрат) - умножение числа самого на себя, в третью степень (в куб) - умножение квадрата числа еще раз на исходное число и т.д. Такого рода перемножение, представляющее собой возведение числа в целую положительную степень, осуществляется просто. При возведении числа в целую, но отрицательную степень, результат представляется дробью, в числителе которой помещается единица, а в знаменателе - возводимое в степень число с тем же, но положительным показателем степени.

По определению

a⁰ = 1,

Из этого определения следует, что для любых натуральных чисел m и n справедливы следующие формулы:

а^та^п = а^т+п, (аⁿ)^т = а^тп, а^пb^п = (ab)ⁿ.

Число, которое при возведении в степень n дает а, называется корнем степени n из а. Если число п нечетное, то существует только один корень степени п из числа а, который обозначается или . Если п четное, а число а — положительное, то корней будет два. Например, числа 3 и -3 будут корнями четвертой степени из 81, т.к. 3⁴ = 81 и (-3)⁴ = 81. Положительный корень называется арифметическим и именно он обозначается символом или .

Степень с дробным показателем определяется так:

Для уменьшения трудоемкости выполнения операций умножения, деление чисел (особенно многозначных), возведения чисел в любые степени, извлечение корней и т.д. часто применяют логарифмирование.

Логарифмом числа «N» по основанию «а» называется показатель степени, в которую нужно возвести а, чтобы получить число N.

Обозначение логарифма:

log _a N = x или a ^x = N

По определению логарифма справедливо равенство

,

из которого на основе свойств показательной функции устанавливаются основные свойства логарифмов ( здесь M, N, и k – положительные числа):

,

,

,

.

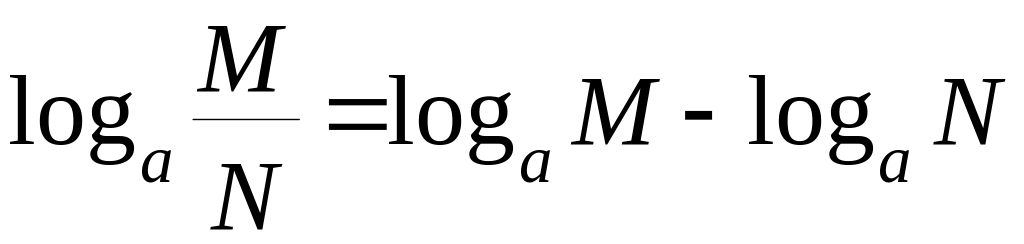Эти свойства позволяют сводить умножение и деление чисел (представленных в виде степеней некоторого числа, принятого за основание) к сложению и вычитанию показателей степеней, а возведение в степень и извлечение корня – к умножению и делению на показатель степени, поэтому применение логарифмов упрощает и сокращает сложные вычисления.

При нашей десятичной системе счисления самым удобным основанием является число 10. Логарифмы по основанию 10 называется десятичным логарифмом и обозначается lg:

При основании, равным 10, только логарифмы целых степеней чисел 10 представляются целыми числами ( ), логарифмы же остальных чисел представляются дробями, и в таблицах даются их приближенные значения в виде ко­нечных десятичных дробей, например lg25,43= 1,4053. Целая часть значения лога­рифма называется характеристикой, дроб­ная - мантиссой.

Любое положительное число N всегда можно представить в виде N = 10ⁿ • х, где п- целое число, а х заключено в пределах oт 1 до 10. Заметим, что lg 1 = 0, lg 10=1, а для любого числа х, заключенного между 1 и 10 его логарифм заключен между нулем и единицей: 0<lgx<l. Из этого представления числа N следует, что lgN=n+lgx, где n-характеристика, а lg х-мантисса логарифма числа N.

Характеристику числа определяют по его виду. Для числа, большего единицы, характеристика на единицу меньше числа цифр у целой части этого числа. Для числа, заключенного между нулем и единицей и записанной десятичной дробью, характеристика отрицательна и равна взятому со знаком минус числу нулей до первой значащей цифры, например для числа 0,0216 его характеристика равна — 2. Благодаря такому простому способу определения характеристики в таблицах даются одни мантиссы.

Логарифмы были введены шотландским математиком Дж. Непером (1550-1617) и независимо от него швейцарским механике» и математиком И. Бюрги (1552-1632). Бюрги пришел к логарифмам раньше, но опубликовал свои таблицы с опозданием (в 1620 г.). и первой в 1614 г. появилась работа Непера «Описание удивительной таблицы логариф­мов». Основанием таблицы логарифмов Не­пера является иррациональное число, к кото­рому неограниченно приближаются числа вида (1 + 1/n)ⁿ при безграничном возрастании п. Это число называют неперовым числом и со времен Л. Эйлера обозначают буквой е:

.

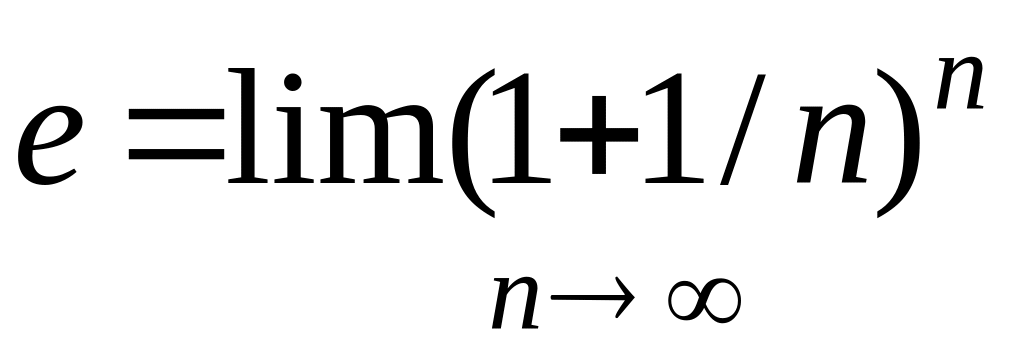Непер составил таблицы, взяв очень хоро­шее приближение числа е, а именно . Логарифмы по основанию е назы­ваются натуральными логарифмами и обо­значаются In (образовано от первых букв слов «логарифм натуральный»).

Первые таблицы десятичных логарифмов были составлены необыкновенно изобрета­тельным и остроумным вычислителем, ан­глийским математиком Г. Бриггсом (1561-1630). Его «логарифмическая арифмети­ка» содержала четырнадцатизначные таблицы для чисел от 1 до 20000 и от 90000 до 100000. Голландский математик А. Флакк (1600-1667) заполнил пробелы бриггсовых таблиц, напе­чатав в 1628 г. таблицы логарифмов всех чи­сел от 1 до 100000 с десятью знаками в ман­тиссе. Эти таблицы стали выпускаться во многих странах мира. На русском языке первые логарифмические таблицы были из­даны в 1703 г.

При различных вычислениях большей частью принято пользоваться десятичной системой счисления, содержащей 10 цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Однако эта система при расчетах на ЭВМ уступает место двоичной системе - такой, где есть только две цифры: ноль и единица.

В десятичной системе число можно записать, используя степень основания, например так:

2839 = 2 * 10³ + 8 * 10² + 3 * 10¹ + 9 * 10⁰.

В двоичной системе счисления любое число можно изобразить, например так:

43 = 1 * 2⁵ + 0 * 2⁴ + 1 * 2³ + 0 * 2² + 1 * 2¹ + 1 * 2⁰ или 101011

Применение двоичной сиcтемы счисления в ЭВМ обусловлено тем, что электронные машины - это сложные электрические схемы, а самым простым случаем «срабатывания» любой электрической схемы будет появление тока в проводнике, либо прекращение прохождения тока по проводнику. Можно условиться, что если ток есть, обозначаем это «1», а если тока нет - «0». В результате создается простая возможность кодировать двоичные числа комбинациями создания в электронных схемах импульсов электрического тока и пауз между импульсами.

Двоичная система счисления позволяет легко кодировать различные сообщения. Любое сообщение может быть выражено в двоичной системе, в виде «да» (или «1») и «нет» (или «0»). Если сообщение написано, например, словами, имеющимися в словаре, то можно найти каждое слово в словаре, задавая сначала такой вопрос: находится ли оно в первой половине словаря или нет? Пусть оно помещено в первой половине словаря. Тогда это обозначим цифрой «1». Далее будет задан вопрос: находится ли искомое слово в первой половине первой части словаря. Если ответ окажется положительным, то обозначим цифрой «1», если отрицательным - «0» и т.д. Такая система запросов позволит, например, закодировать слово в словаре из 250 тыс. слов самое большее восемнадцатью вопросами с ответами «1» или «0», то есть набором из восемнадцати двоичных цифр.

Аналогично этому, можно просто закодировать с помощью «1» и «0» все, что должно быть введено в ЭВМ, что ЭВМ должна обработать.