35. Преобразование «звезды» сопротивлений в «треугольник» сопротивлений и наоборот.

Найдем условия эквивалентности двух участков электрической цепи, которые представляют собой соединение пассивных идеализированных двухполюсников треугольником и звездой. По определению, эти участки цепи эквивалентны, если при замене одного участка другим токи выводов , , 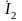и напряжения между выводами , , останутся неизмен­ными. Учитывая, что из трех напряжений между вывода­ми только два являются независимыми (третье может быть получено из уравнения баланса напряжений), для эквивалентности треуголь­ника сопротивлений звезде достаточно потребовать, чтобы любая пара из трех напряжений между вывода одной цепи была равна соответствующей паре напряжений другой цепи (при одинаковых значениях токов внешних выводов).

Выразим токи сопротивлений , , образующих сторо­ны треугольника сопротивлений, через токи внешних выводов , , .Составляя на основании законов Кирхгофа систему уравнений электрического равновесия этого участка цепи:

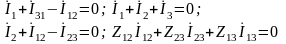
и решая ее относительно токов , , , находим

(1)

Используя выражения (1), определяем напряжения между внешними выводами треугольника сопротивлений:

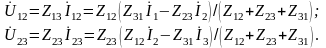
Соответствующие напряжения между внешними выводами звез­ды:

Приравнивая напряжения и между внешними выводами рассматриваемых участков цепи получаем:

(2)

В соответствии с изложенным равенства (2) должны выпол­няться при любых значениях токов внешних вывод. Полагая в (2) сначала , а затем , определяем соотношения между сопротивлениями, при которых рассматриваемые участки цепей эквивалентны:

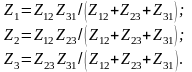(3)

Рассчитав сопротивления , , по заданным , , , можно осуществить эквивалентную замену треугольника сопротив­лений звездой (преобразование треугольник — звезда). При этом преобразовании из цепи устраняется контур, образуемый сопротивлениями , , и появляется новый узел — место соединения сопротивлений , , .

Решая систему уравнений (3) относительно , , , получаем соотношения, позволяющие производить эквивалентную замену звезды сопротивлений треугольником (преобразование звез­да — треугольник):

(4)

Преобразование звезда — треугольник приводит к уменьшению числа узлов преобразуемой цепи (за счет устранения узла, явля­ющегося местом соединения сопротивлений , , ), однако при этом появляется новый контур, образуемый сопротивлениями , , .

Заменим в выражениях (4) комплексные сопротивления эле­ментов их проводимостями. Проведя преобразования, установим, что выражения для комплексных проводимостей элементов, образу­ющих стороны треугольника,

(5)

имеют такую же структуру, как и выражения для комплексных сопротивлений, входящих в лучи звезды (3). Подобным образом можно получить выражения для комплексных проводимостей лучей звезды 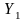, , , которые оказываются аналогичными выражени­ям для комплексных сопротивлений сторон треугольника (4).

Выражения (5) могут быть обобщены и для преобразования N-лучевой звезды в N-угольник:

где — проводимость стороны N-угольника, соединяющей узлы —проводимости элементов, образующих лучи звезды.

Обратное преобразование полного N-угольника в N-лучевую звезду в общем случае невозможно.

Применение преобразований треугольник — звезда и звезда — треугольник в ряде случаев позволяет существенно упростить ана­лиз цепей, в частности иногда с помощью этих преобразований удается приводить сложные участки цепей к более простым, представляющим собой параллельное, последовательное или смешанное соединение элементов.