28. Анализ простейших линейных цепей при гармоническом воздействии. Последовательная rс - цепь.

Рассмотрим последовательную RC –цепь, к зажимам которой приложено напряжение u, изменяющееся по гармоничес­кому закону. Найдем комплексный ток цепи и ее комплексное входное сопротивление.

Переходя к комплексной схеме замещения цепи и используя законы Ома и Кирхгофа в комплексной форме, состав­ляем систему уравнений электрического равновесия цепи:

.

, (1)

где и — комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему уравнений (1) относительно комплексного действующего значения искомого тока, получаем:

, (2)

где — комплексное входное сопротивление цепи, кото­рое равно сумме комплексных сопротивлений последовательно включенных идеализированных элементов. Комплексная схема за­мещения цепи, соответствующая уравнению (2), приведена на рис. 2.19, в. Выразим комплексное сопротивление цепи Z через параметры входящих в цепь элементов:

, (3)

где .

Как следует из выражения (3), при конечных значениях , R и C угол лежит в пределах , т. е. входное сопротив­ление цепи имеет резистивно-емкостный характер. Окончательно уравнения имеют вид:

. (4)

Ток i опережает приложенное напряжение и по фазе на угол .

29. Анализ простейших линейных цепей при гармоническом воздействии. Последовательная RLС-цепь. Рассмотрим последовательную RLC-цепь , находя­щуюся под гармоническим воздействием. Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесия цепи:

(1)

где — комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (1) относительно тока , получаем:

(2)

Комплексное входное сопротивление Z последовательной RLC-цепи равно сумме комплексных сопротивлений входящих в цепь элементов и определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:

. (3)

Переходя от алгебраической формы записи Z к показательной, находим модуль и аргумент комплексного входного сопротивления:

. (4)

Из выражений (4) следует, что характер входного сопротивле­ния цепи зависит от соотношения между мнимыми составляющими комплексного входного сопротивления емкости и индуктивности . При входное сопротивление цепи имеет резистивно-индуктивный характер . Если , то входное сопротивле­ние цепи имеет резистивно-емкостный характер . При мнимые составляющие входного сопротивле­ния емкости и индуктивности взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер .

Вектор , изображающий напряжение на со­противлении совпадает по направлению с вектором ; вектор 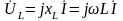повернут относительно на 90° против часовой стрелки; вектор направлен противоположно вектору . При вектор совпадает по направлению с вектором , ток цепи отстает по фазе от напряже­ния . При вектор совпадает по направлению с вектором , ток цепи опережает по фазе напряже­ние . Если , то вектор , напря­жение на зажимах цепи равно напряжению на сопротивлении , ток цепи совпадает по фазе с приложенным напряжением .